Grover’s Search Algorithm [1]¶
In 1996 Lov Grover [2] introduced a novel search algorithm which exhibits quadratic speedup and uses a technique called amplitude amplification. Imagine that we are given a printed phone book and asked to find to whom a particular phone number is associated. Phone directories are usually arranged alpabetically. We have to go through each entry in the phone directory to determine whom the phone number belongs.
At an average, it may take \(N/2\) attempts to find the right answer, which is somewhat difficult if the phone book is large. This type of search is called unstructured because we do not have any guarantee that the database is sorted in an usable fashion. Grover’s algorithm solves the problem of unstructured search. Grover’s algorithm takes a number corresponding to an entry in the database as its input and performs a test to see if this is the special value \(ω\) being searched for. This search is done in about \(\frac{\pi}{4} \sqrt[]{N}\) steps, a quadratic speedup compared to the classical algorithm described above.
The Grover’s search is defined as follows.
Given a set of \(N\) elements forming a set \(X= \{x_1,x_2,x_3,\cdots,x_N \}\), and given a boolean function \(f:X →\{0,1\}\), the goal is to find an element \(ω\) in \(X\) such that \(f(ω)=1\).
Before going through the algorithm, let us make some assumptions.
The element ω, which satisfies the equation \(f(ω)=1\), is unique. We shall relax this condition at the end of the discussion.
The size of the database is a power of \(2\), i.e., \(N= 2^n\). Some padding may be required to achieve this.
The data is labeled as \(n\)-bit Boolean strings \(\left\{0,1\right\}^n\).
The Boolean function \(f\) maps \(\left\{0,1\right\}^n\) to \(\left\{0,1\right\}\).
Let us assume that we define an oracle function \(\hat{O}\) which produces a transformation function: \(\hat{O}|x\rangle ⟶ |f(x)\rangle\). Unfortunately, this is not unitary, as it takes an \(n\)-bit string and produces a single bit as an output. The solution is to use an oracle black-box function as follows:
The following figure shows the block diagram of the Grover’s search algorithm.
As shown in the diagram, Grover’s search starts with all qubits initialized to state \(|0\rangle\). Then a Walsh-Hadamard transform puts the qubits in an equal superposition state. The state of the system can be written as follows.
All the qubits have the same amplitude \(\frac{1}{\sqrt{N}}\) at this stage. The following bar graph illustrates this stage.
The next step is to apply the oracle \(\hat{O}\). The oracle function negates the amplitude of the state \(ω\). The rest of the states remain unaffected by the oracle. The following equation shows the new system state:
The following graph shows the amplitudes of all possible states:
The mean of the amplitudes \(μ\) is given by the following standard equation.
where \(a_x\) is the amplitude of a given \(x\) in the range \(\{0,1\}^n\). We can expand this equation to calculate the value of \(μ\) at this stage. The mean of the amplitudes is now given by the following equation.
Hence, the amplitude for most terms is approximately \(\frac{1}{\sqrt{N}}\). It has not significantly changed and it is relatively insignificant for large values of \(n\).The next stage in the quantum circuit is called the Grover diffusion operator (also called amplitude purification).
The Grover diffusion operator performs the following mapping:
The system state at this stage is given by the following graph:
We find that the system states almost remain the same, except for the state \(ω\). The amplitude of \(ω\) gets amplified by a factor of about \(\frac{3}{\sqrt{N}}\). The combination of these two steps – the oracle function followed by the Grover Diffusion Operator – is called Grover Iteration.
To amplify \(ω\) further, let us apply the Grover Iteration one more time. The following graph illustrates the state of the system after the second iteration:
The graph shows that the amplitude of \(ω\) gets magnified linearly \(~\frac{t}{\sqrt{N}}\) with each iteration ( \(t\) being the number of solutions.) By applying this cycle for \(O(\sqrt{N})\) times, the amplitude of \(ω\) should exceed a threshold value. Beyond that point, the large negative amplitude of \(ω\) (when the oracle \(\hat{O}\) flips it) can reduce the overall mean value causing a reduction in the amplitude when the Grover Diffusion Operator is applied.
Note that Grover’s algorithm magnifies the amplitude and not the probability amplitude. With \(O(\sqrt{N})\) iterations, the Grover algorithm solves the problem, whereas a classical solution requires \(O(N)\) steps. This quadratic speedup is because quantum parallelism computes \(f(x)\) for all the \(N= 2^n\) states in parallel. If in case there are multiple solutions \(k\) to the problem, we would need \(O(\sqrt{N/k})\) iterations.
Example Implementation
As an example, the following code implement a 3-qubit version of Grover’s algorithm based on the oracle function and the Grover diffusion operator defined by C. Figgatt [6] et al.
The oracle function:
The example oracle function implements a unitary transformation function \(\hat{O}\) that acts on an \(n\)-qubit input register and a \(1\) qubit output register. The function applies an \(X\) gate to the output register when the input register is equal to \(ω\). We can write this transformation as follows:
This function can be implemented as a multi-control Toffoli gate.
The following figure illustrates a \(3\)-qubit oracle with a hidden value of \(ω=010\). The Toffoli gate switches the target (i.e., the output register), when all control registers are in state \(|1\rangle\). For the circuit shown below, this is when \(|x\rangle=010\).
The quantum circuit for implementing the Grover Diffusion Operator is given in the following diagram :
Example Code
Note
Be sure to use your API token and your account name.
Step 1. Import the required modules and obtain the backend
import QuantumRingsLib
from QuantumRingsLib import QuantumRegister, AncillaRegister, ClassicalRegister, QuantumCircuit
from QuantumRingsLib import QuantumRingsProvider
from QuantumRingsLib import job_monitor
from QuantumRingsLib import JobStatus
from matplotlib import pyplot as plt
import numpy as np
provider = QuantumRingsProvider(token =<YOUR_TOKEN_HERE>, name=<YOUR_ACCOUNT_NAME_HERE>)
backend = provider.get_backend("scarlet_quantum_rings")
shots = 100
provider.active_account()
Step 2. Define the core methods
def ccz(qc, control1, control2, target):
"""
The CCZ gate or the doubly controlled Z-gate.
This gate flips the phase of the target qubit if the control qubits are in |11> state.
Args:
qc (QuantumCircuit):
The quantum Circuit to use.
control1 (int):
The index number of the first control qubit.
control2 (int):
The index number of the second control qubit.
target (int):
The index number of the target qubit, where the transform is applied
Returns:
None
"""
qc.h(target)
qc.ccx(control1, control2, target)
qc.h(target)
return
def cccx(qc,control1, control2, control3, anc, target):
"""
The three control Toffoli gate.
An X gate is applied to the target qubit, if the control qubits are in state |111>.
Args:
qc (QuantumCircuit):
The quantum Circuit to use.
control1 (int):
The index number of the first control qubit.
control2 (int):
The index number of the second control qubit.
control3 (int):
The index number of the third control qubit
anc (int):
The index number of a temporary worker qubit
target (int):
The index number of the target qubit, where the transform is applied
Returns:
None
"""
qc.ccx(control1, control2, anc)
qc.ccx(control3, anc, target)
qc.ccx(control1, control2, anc)
qc.ccx(control3, anc, target)
return
def grover_oracle( qc, x0, x1, x2, anc, y):
"""
The Grover's Oracle
Args:
qc (QuantumCircuit):
The quantum Circuit to use.
x0 (int):
The index number of the first qubit of the x register.
x1 (int):
The index number of the second qubit of the x register.
x2 (int):
The index number of the third qubit of the x register.
anc (int):
The index number of a temporary work qubit
y (int):
The index number of the target qubit, where the transform is applied
Returns:
None.
"""
qc.x(x2)
qc.x(x0)
cccx(qc, x0, x1, x2, anc, y)
qc.x(x0)
qc.x(x2)
def grover_diffusion_operator(qc, x0, x1, x2, y):
"""
The 3-qubit diffusion operator for Grover's algorith.
Args:
x0 (int):
The index number of the first qubit of the x register.
x1 (int):
The index number of the second qubit of the x register.
x2 (int):
The index number of the third qubit of the x register.
y (int):
The index number of the target qubit, where the transform is applied
Returns:
None.
"""
qc.h(x0)
qc.h(x1)
qc.h(x2)
qc.h(y) # Bring this back to state 1 for next stages
qc.x(x0)
qc.x(x1)
qc.x(x2)
ccz(qc, x0, x1, x2 )
qc.x(x0)
qc.x(x1)
qc.x(x2)
qc.h(x0)
qc.h(x1)
qc.h(x2)
def plot_histogram (counts, title=""):
"""
Plots the histogram of the counts
Args:
counts (dict):
The dictionary containing the counts of states
titles (str):
A title for the graph.
Returns:
None
"""
fig, ax = plt.subplots(figsize =(10, 7))
plt.xlabel("States")
plt.ylabel("Counts")
mylist = [key for key, val in counts.items() for _ in range(val)]
unique, inverse = np.unique(mylist, return_inverse=True)
bin_counts = np.bincount(inverse)
plt.bar(unique, bin_counts)
maxFreq = max(counts.values())
plt.ylim(ymax=np.ceil(maxFreq / 10) * 10 if maxFreq % 10 else maxFreq + 10)
# Show plot
plt.title(title)
plt.show()
return
Step 3. Putting everything together.
#
# Grover's algorithm
#
q = QuantumRegister(3 , 'x')
y = QuantumRegister(1 , 'y')
anc = QuantumRegister(1 , 'a')
c = ClassicalRegister(3 , 'c')
qc = QuantumCircuit(q, y, anc, c)
qc.x(y[0])
qc.h(q[0])
qc.h(q[1])
qc.h(q[2])
qc.h(y[0])
grover_oracle (qc, q[0], q[1], q[2], anc[0], y[0])
grover_diffusion_operator (qc, q[0], q[1], q[2], y[0])
grover_oracle (qc, q[0], q[1], q[2], anc[0], y[0])
grover_diffusion_operator (qc, q[0], q[1], q[2], y[0])
grover_oracle (qc, q[0], q[1], q[2], anc[0], y[0])
grover_diffusion_operator (qc, q[0], q[1], q[2], y[0])
qc.measure(q[0],c[0])
qc.measure(q[1],c[1])
qc.measure(q[2],c[2])
job = backend.run(qc, shots=shots)
job_monitor(job)
result = job.result()
counts = result.get_counts()
print (counts)
del q, y, anc
del c
del qc
del result
del job
plot_histogram(counts, "")
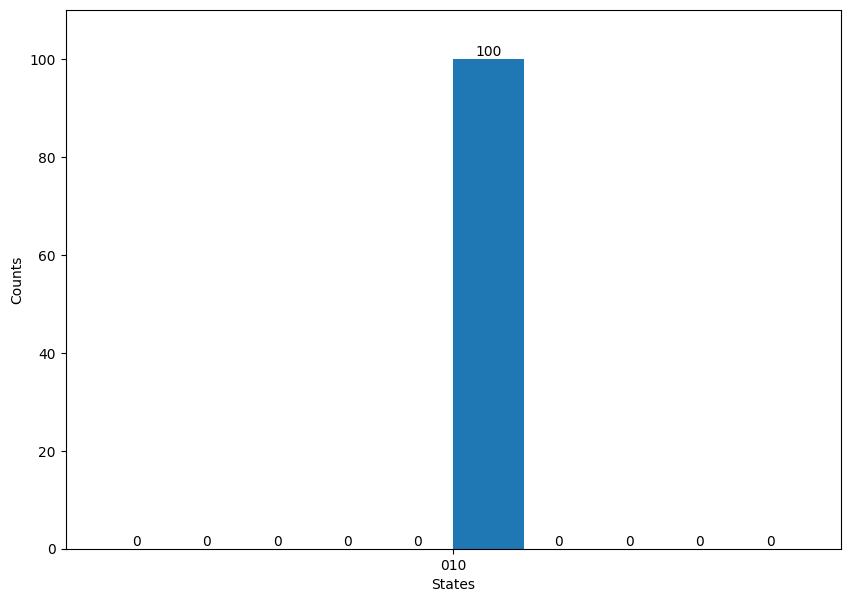
A sample histogram showing the amplification of \(ω\) to the desired level is shown below. The results could be different for you.
Footnotes