02 - Neural Network Classifier & Regressor
[1]:
#This code found at:
#https://qiskit-community.github.io/qiskit-machine-learning/tutorials/02_neural_network_classifier_and_regressor.html
[2]:
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit import Parameter
from qiskit.circuit.library import RealAmplitudes, ZZFeatureMap
from qiskit_machine_learning.optimizers import COBYLA, L_BFGS_B
from qiskit_machine_learning.utils import algorithm_globals
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier, VQC
from qiskit_machine_learning.algorithms.regressors import NeuralNetworkRegressor, VQR
#from qiskit_machine_learning.neural_networks import SamplerQNN, EstimatorQNN
from qiskit_machine_learning.circuit.library import QNNCircuit
from quantumrings.toolkit.qiskit.machine_learning import QrEstimatorQNN as EstimatorQNN
from quantumrings.toolkit.qiskit.machine_learning import QrSamplerQNN as SamplerQNN
[3]:
num_inputs = 2
num_samples = 20
X = 2 * algorithm_globals.random.random([num_samples, num_inputs]) - 1
y01 = 1 * (np.sum(X, axis=1) >= 0) # in { 0, 1}
y = 2 * y01 - 1 # in {-1, +1}
y_one_hot = np.zeros((num_samples, 2))
for i in range(num_samples):
y_one_hot[i, y01[i]] = 1
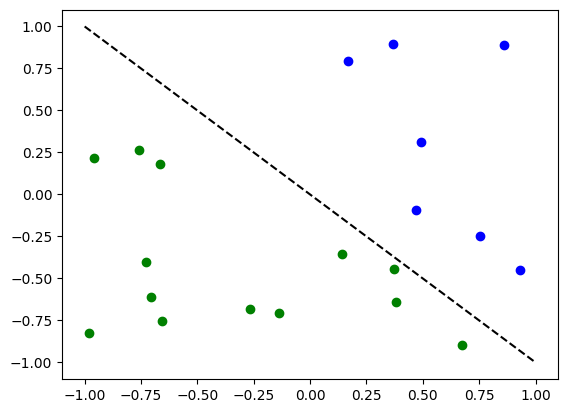
for x, y_target in zip(X, y):
if y_target == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
[4]:
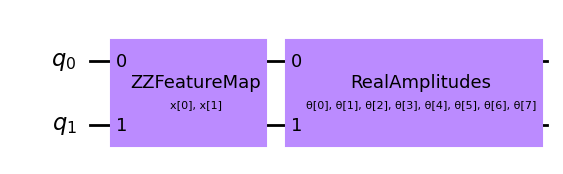
# construct QNN with the QNNCircuit's default ZZFeatureMap feature map and RealAmplitudes ansatz.
qc = QNNCircuit(num_qubits=2)
qc.draw("mpl", style="clifford")
[4]:
[5]:
estimator_qnn = EstimatorQNN(circuit=qc)
[6]:
# QNN maps inputs to [-1, +1]
estimator_qnn.forward(X[0, :], algorithm_globals.random.random(estimator_qnn.num_weights))
[6]:
array([[0.22695227]])
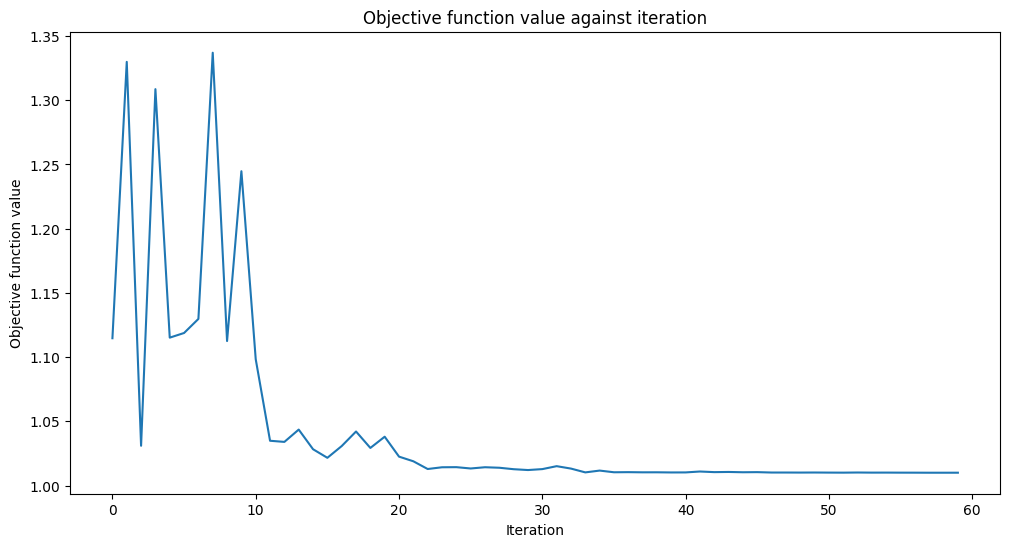
[7]:
# callback function that draws a live plot when the .fit() method is called
def callback_graph(weights, obj_func_eval):
clear_output(wait=True)
objective_func_vals.append(obj_func_eval)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
[8]:
# construct neural network classifier
estimator_classifier = NeuralNetworkClassifier(
estimator_qnn, optimizer=COBYLA(maxiter=60), callback=callback_graph
)
[9]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
estimator_classifier.fit(X, y)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
estimator_classifier.score(X, y)
[9]:
0.55
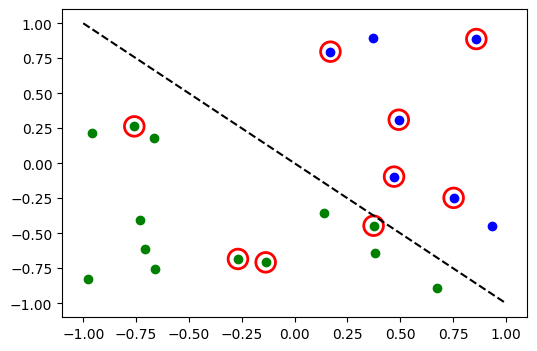
[10]:
# evaluate data points
y_predict = estimator_classifier.predict(X)
# plot results
# red == wrongly classified
for x, y_target, y_p in zip(X, y, y_predict):
if y_target == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
if y_target != y_p:
plt.scatter(x[0], x[1], s=200, facecolors="none", edgecolors="r", linewidths=2)
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
[11]:
estimator_classifier.weights
[11]:
array([0.70970272, 1.76196821, 0.03518958, 0.6172359 , 0.06227224,
0.47601816, 0.45671342, 0.55066885])
[12]:
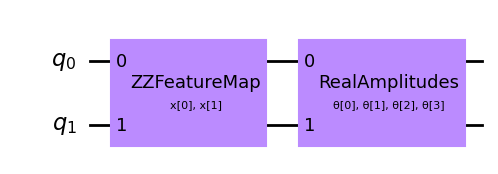
# construct a quantum circuit from the default ZZFeatureMap feature map and a customized RealAmplitudes ansatz
qc = QNNCircuit(ansatz=RealAmplitudes(num_inputs, reps=1))
qc.draw("mpl", style="clifford")
[12]:
[13]:
# parity maps bitstrings to 0 or 1
def parity(x):
return "{:b}".format(x).count("1") % 2
output_shape = 2 # corresponds to the number of classes, possible outcomes of the (parity) mapping.
[14]:
# construct QNN
sampler_qnn = SamplerQNN(
circuit=qc,
interpret=parity,
output_shape=output_shape,
)
[15]:
# construct classifier
sampler_classifier = NeuralNetworkClassifier(
neural_network=sampler_qnn, optimizer=COBYLA(maxiter=30), callback=callback_graph
)
[16]:
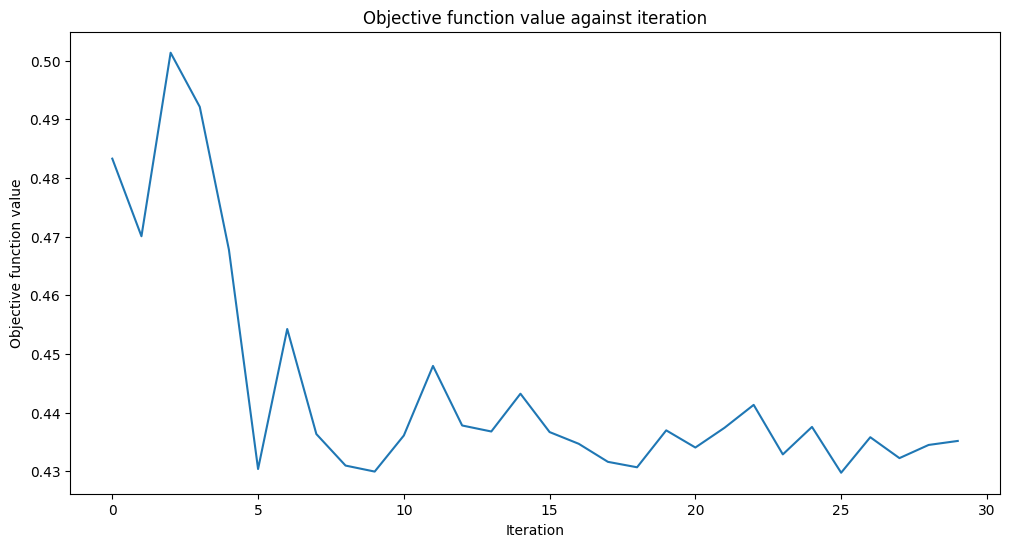
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
sampler_classifier.fit(X, y01)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
sampler_classifier.score(X, y01)
[16]:
0.7
[17]:
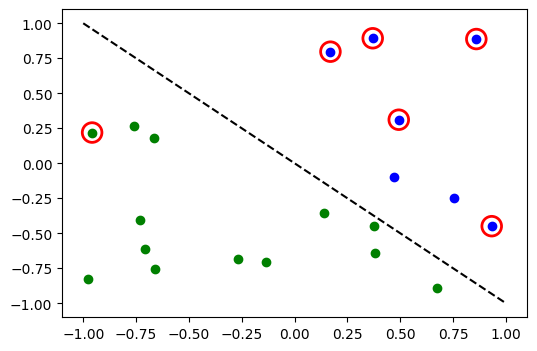
# evaluate data points
y_predict = sampler_classifier.predict(X)
# plot results
# red == wrongly classified
for x, y_target, y_p in zip(X, y01, y_predict):
if y_target == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
if y_target != y_p:
plt.scatter(x[0], x[1], s=200, facecolors="none", edgecolors="r", linewidths=2)
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
[18]:
sampler_classifier.weights
[18]:
array([ 2.28192843, 0.30937412, -0.10382305, 1.82800473])
[19]:
# construct feature map, ansatz, and optimizer
feature_map = ZZFeatureMap(num_inputs)
ansatz = RealAmplitudes(num_inputs, reps=1)
# construct variational quantum classifier
vqc = VQC(
feature_map=feature_map,
ansatz=ansatz,
loss="cross_entropy",
optimizer=COBYLA(maxiter=30),
callback=callback_graph,
)
[20]:
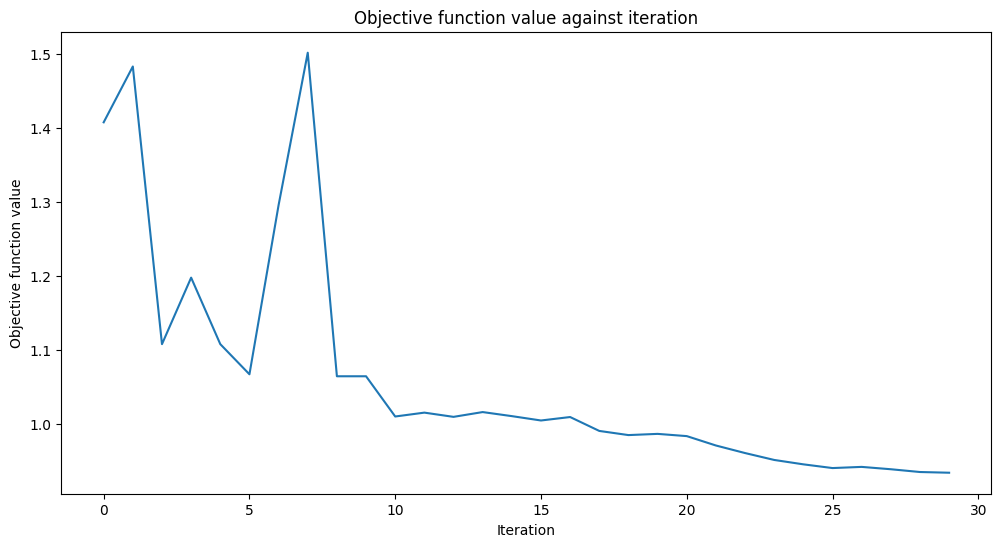
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
vqc.fit(X, y_one_hot)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
vqc.score(X, y_one_hot)
[20]:
0.6
[21]:
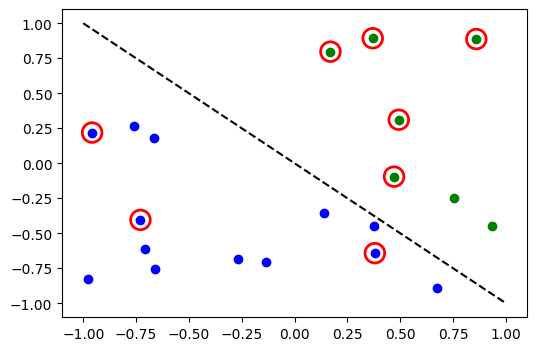
# evaluate data points
y_predict = vqc.predict(X)
# plot results
# red == wrongly classified
for x, y_target, y_p in zip(X, y_one_hot, y_predict):
if y_target[0] == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
if not np.all(y_target == y_p):
plt.scatter(x[0], x[1], s=200, facecolors="none", edgecolors="r", linewidths=2)
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
[22]:
from sklearn.datasets import make_classification
from sklearn.preprocessing import MinMaxScaler
X, y = make_classification(
n_samples=10,
n_features=2,
n_classes=3,
n_redundant=0,
n_clusters_per_class=1,
class_sep=2.0,
random_state=algorithm_globals.random_seed,
)
X = MinMaxScaler().fit_transform(X)
[23]:
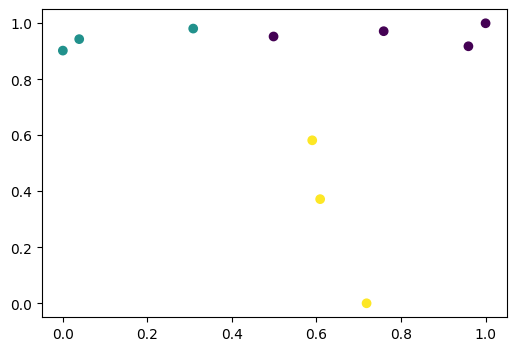
plt.scatter(X[:, 0], X[:, 1], c=y)
[23]:
<matplotlib.collections.PathCollection at 0x2963b41edd0>
[24]:
y_cat = np.empty(y.shape, dtype=str)
y_cat[y == 0] = "A"
y_cat[y == 1] = "B"
y_cat[y == 2] = "C"
print(y_cat)
['B' 'A' 'A' 'C' 'A' 'B' 'A' 'C' 'B' 'C']
[25]:
vqc = VQC(
num_qubits=2,
optimizer=COBYLA(maxiter=30),
callback=callback_graph,
)
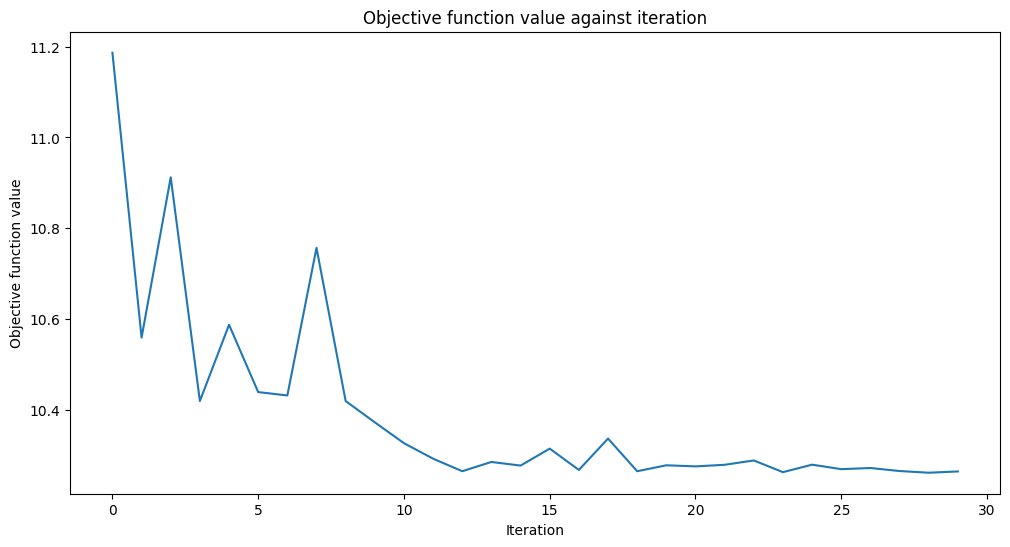
[26]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
vqc.fit(X, y_cat)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
vqc.score(X, y_cat)
[26]:
0.6
[27]:
predict = vqc.predict(X)
print(f"Predicted labels: {predict}")
print(f"Ground truth: {y_cat}")
Predicted labels: ['B' 'A' 'A' 'B' 'A' 'A' 'A' 'A' 'B' 'A']
Ground truth: ['B' 'A' 'A' 'C' 'A' 'B' 'A' 'C' 'B' 'C']
[28]:
num_samples = 20
eps = 0.2
lb, ub = -np.pi, np.pi
X_ = np.linspace(lb, ub, num=50).reshape(50, 1)
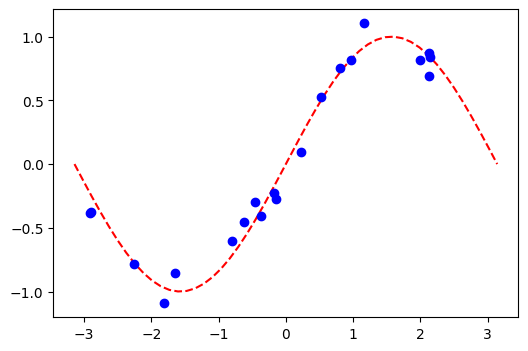
f = lambda x: np.sin(x)
X = (ub - lb) * algorithm_globals.random.random([num_samples, 1]) + lb
y = f(X[:, 0]) + eps * (2 * algorithm_globals.random.random(num_samples) - 1)
plt.plot(X_, f(X_), "r--")
plt.plot(X, y, "bo")
plt.show()
[29]:
# construct simple feature map
param_x = Parameter("x")
feature_map = QuantumCircuit(1, name="fm")
feature_map.ry(param_x, 0)
# construct simple ansatz
param_y = Parameter("y")
ansatz = QuantumCircuit(1, name="vf")
ansatz.ry(param_y, 0)
# construct a circuit
qc = QNNCircuit(feature_map=feature_map, ansatz=ansatz)
# construct QNN
regression_estimator_qnn = EstimatorQNN(circuit=qc)
[30]:
# construct the regressor from the neural network
regressor = NeuralNetworkRegressor(
neural_network=regression_estimator_qnn,
loss="squared_error",
optimizer=L_BFGS_B(maxiter=5),
callback=callback_graph,
)
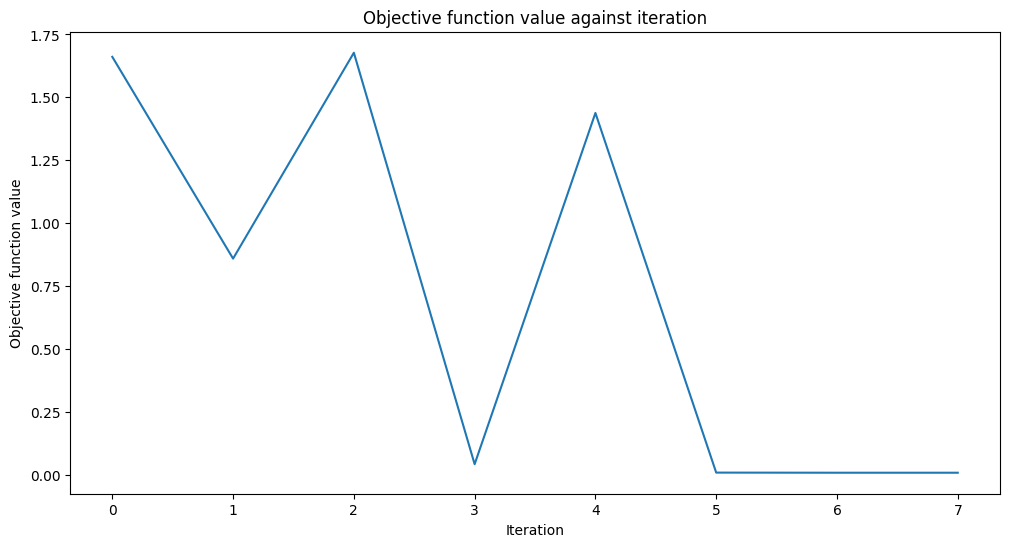
[31]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit to data
regressor.fit(X, y)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score the result
regressor.score(X, y)
[31]:
0.9770123329492192
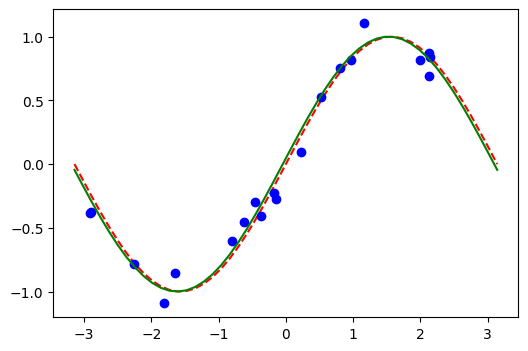
[32]:
# plot target function
plt.plot(X_, f(X_), "r--")
# plot data
plt.plot(X, y, "bo")
# plot fitted line
y_ = regressor.predict(X_)
plt.plot(X_, y_, "g-")
plt.show()
[33]:
regressor.weights
[33]:
array([-1.52551382])
[34]:
vqr = VQR(
feature_map=feature_map,
ansatz=ansatz,
optimizer=L_BFGS_B(maxiter=5),
callback=callback_graph,
)
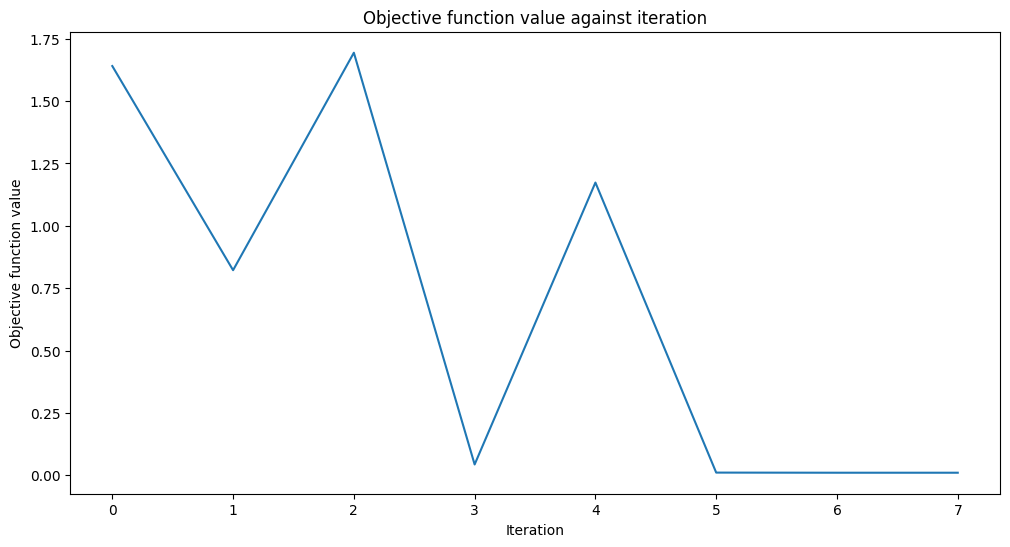
[35]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit regressor
vqr.fit(X, y)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score result
vqr.score(X, y)
[35]:
0.9770123329492196
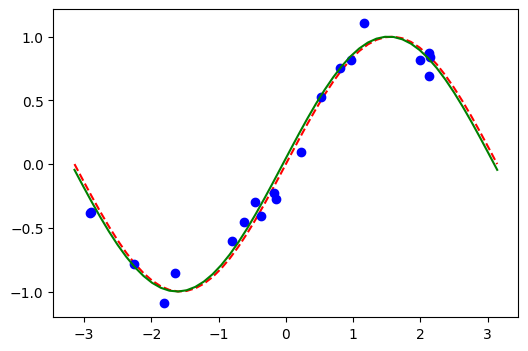
[36]:
# plot target function
plt.plot(X_, f(X_), "r--")
# plot data
plt.plot(X, y, "bo")
# plot fitted line
y_ = vqr.predict(X_)
plt.plot(X_, y_, "g-")
plt.show()
[ ]: