03 - Minimum Eigen Optimizer
[1]:
# This code is from the tutorial at:
# https://qiskit-community.github.io/qiskit-optimization/tutorials/03_minimum_eigen_optimizer.html
[2]:
from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
# Switch to Quantum Rings's Sampler
#from qiskit.primitives import Sampler
from quantumrings.toolkit.qiskit import QrSamplerV1 as Sampler
from qiskit_optimization.algorithms import (
MinimumEigenOptimizer,
RecursiveMinimumEigenOptimizer,
SolutionSample,
OptimizationResultStatus,
)
from qiskit_optimization import QuadraticProgram
from qiskit.visualization import plot_histogram
from typing import List, Tuple
import numpy as np
[3]:
# create a QUBO
qubo = QuadraticProgram()
qubo.binary_var("x")
qubo.binary_var("y")
qubo.binary_var("z")
qubo.minimize(linear=[1, -2, 3], quadratic={("x", "y"): 1, ("x", "z"): -1, ("y", "z"): 2})
print(qubo.prettyprint())
Problem name:
Minimize
x*y - x*z + 2*y*z + x - 2*y + 3*z
Subject to
No constraints
Binary variables (3)
x y z
[4]:
op, offset = qubo.to_ising()
print("offset: {}".format(offset))
print("operator:")
print(op)
offset: 1.5
operator:
SparsePauliOp(['IIZ', 'IZI', 'ZII', 'IZZ', 'ZIZ', 'ZZI'],
coeffs=[-0.5 +0.j, 0.25+0.j, -1.75+0.j, 0.25+0.j, -0.25+0.j, 0.5 +0.j])
[5]:
qp = QuadraticProgram()
qp.from_ising(op, offset, linear=True)
print(qp.prettyprint())
Problem name:
Minimize
x0*x1 - x0*x2 + 2*x1*x2 + x0 - 2*x1 + 3*x2
Subject to
No constraints
Binary variables (3)
x0 x1 x2
[6]:
algorithm_globals.random_seed = 10598
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 0.0])
exact_mes = NumPyMinimumEigensolver()
[7]:
qaoa = MinimumEigenOptimizer(qaoa_mes) # using QAOA
exact = MinimumEigenOptimizer(exact_mes) # using the exact classical numpy minimum eigen solver
[8]:
exact_result = exact.solve(qubo)
print(exact_result.prettyprint())
objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS
[9]:
qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())
objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS
[10]:
print("variable order:", [var.name for var in qaoa_result.variables])
for s in qaoa_result.samples:
print(s)
variable order: ['x', 'y', 'z']
SolutionSample(x=array([0., 1., 0.]), fval=np.float64(-2.0), probability=0.1220703125, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=np.float64(0.0), probability=0.1640625, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=np.float64(0.0), probability=0.13671875, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=np.float64(1.0), probability=0.076171875, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=np.float64(3.0), probability=0.1552734375, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=np.float64(3.0), probability=0.091796875, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=np.float64(3.0), probability=0.146484375, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 1.]), fval=np.float64(4.0), probability=0.107421875, status=<OptimizationResultStatus.SUCCESS: 0>)
[11]:
def get_filtered_samples(
samples: List[SolutionSample],
threshold: float = 0,
allowed_status: Tuple[OptimizationResultStatus] = (OptimizationResultStatus.SUCCESS,),
):
res = []
for s in samples:
if s.status in allowed_status and s.probability > threshold:
res.append(s)
return res
[12]:
filtered_samples = get_filtered_samples(
qaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)
for s in filtered_samples:
print(s)
SolutionSample(x=array([0., 1., 0.]), fval=np.float64(-2.0), probability=0.1220703125, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=np.float64(0.0), probability=0.1640625, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=np.float64(0.0), probability=0.13671875, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=np.float64(1.0), probability=0.076171875, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=np.float64(3.0), probability=0.1552734375, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=np.float64(3.0), probability=0.091796875, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=np.float64(3.0), probability=0.146484375, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 1.]), fval=np.float64(4.0), probability=0.107421875, status=<OptimizationResultStatus.SUCCESS: 0>)
[13]:
fvals = [s.fval for s in qaoa_result.samples]
probabilities = [s.probability for s in qaoa_result.samples]
[14]:
np.mean(fvals)
[14]:
np.float64(1.5)
[15]:
np.std(fvals)
[15]:
np.float64(1.9364916731037085)
[16]:
samples_for_plot = {
" ".join(f"{qaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
for s in filtered_samples
}
samples_for_plot
[16]:
{'x=0 y=1 z=0': 0.1220703125,
'x=0 y=0 z=0': 0.1640625,
'x=1 y=1 z=0': 0.13671875,
'x=1 y=0 z=0': 0.076171875,
'x=0 y=0 z=1': 0.1552734375,
'x=1 y=0 z=1': 0.091796875,
'x=0 y=1 z=1': 0.146484375,
'x=1 y=1 z=1': 0.107421875}
[17]:
plot_histogram(samples_for_plot)
[17]:
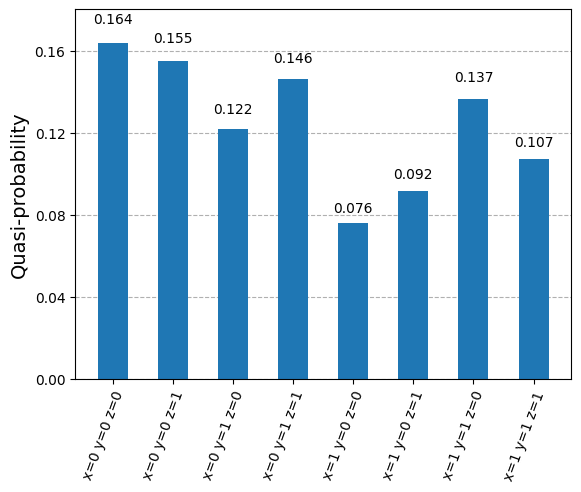
[18]:
rqaoa = RecursiveMinimumEigenOptimizer(qaoa, min_num_vars=1, min_num_vars_optimizer=exact)
[19]:
rqaoa_result = rqaoa.solve(qubo)
print(rqaoa_result.prettyprint())
objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS
[20]:
filtered_samples = get_filtered_samples(
rqaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)
[21]:
samples_for_plot = {
" ".join(f"{rqaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
for s in filtered_samples
}
samples_for_plot
[21]:
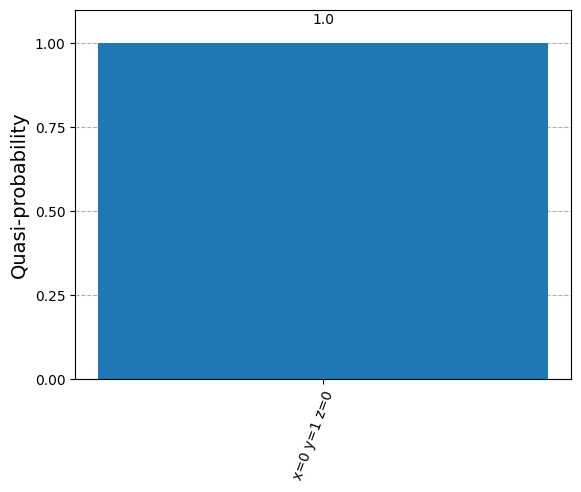
{'x=0 y=1 z=0': 1.0}
[22]:
plot_histogram(samples_for_plot)
[22]:
[ ]: