06 - Max-Cut and Traveling Salesman Problem
[1]:
# This code is from the tutorial at:
# https://qiskit-community.github.io/qiskit-optimization/tutorials/06_examples_max_cut_and_tsp.html
[2]:
# useful additional packages
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx
from qiskit.circuit.library import TwoLocal
from qiskit_optimization.applications import Maxcut, Tsp
from qiskit_algorithms import SamplingVQE, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import SPSA
from qiskit_algorithms.utils import algorithm_globals
# Switch to Quantum Rings's Sampler
#from qiskit.primitives import Sampler
from quantumrings.toolkit.qiskit import QrSamplerV1 as Sampler
from qiskit_optimization.algorithms import MinimumEigenOptimizer
Max-Cut problem
[3]:
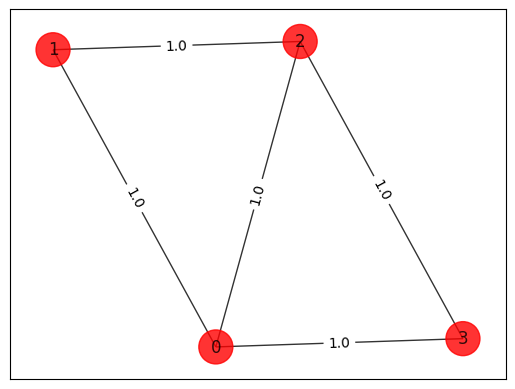
# Generating a graph of 4 nodes
n = 4 # Number of nodes in graph
G = nx.Graph()
G.add_nodes_from(np.arange(0, n, 1))
elist = [(0, 1, 1.0), (0, 2, 1.0), (0, 3, 1.0), (1, 2, 1.0), (2, 3, 1.0)]
# tuple is (i,j,weight) where (i,j) is the edge
G.add_weighted_edges_from(elist)
colors = ["r" for node in G.nodes()]
pos = nx.spring_layout(G)
def draw_graph(G, colors, pos):
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G, node_color=colors, node_size=600, alpha=0.8, ax=default_axes, pos=pos)
edge_labels = nx.get_edge_attributes(G, "weight")
nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=edge_labels)
draw_graph(G, colors, pos)
[4]:
# Computing the weight matrix from the random graph
w = np.zeros([n, n])
for i in range(n):
for j in range(n):
temp = G.get_edge_data(i, j, default=0)
if temp != 0:
w[i, j] = temp["weight"]
print(w)
[[0. 1. 1. 1.]
[1. 0. 1. 0.]
[1. 1. 0. 1.]
[1. 0. 1. 0.]]
Brute force approach
[5]:
best_cost_brute = 0
for b in range(2**n):
x = [int(t) for t in reversed(list(bin(b)[2:].zfill(n)))]
cost = 0
for i in range(n):
for j in range(n):
cost = cost + w[i, j] * x[i] * (1 - x[j])
if best_cost_brute < cost:
best_cost_brute = cost
xbest_brute = x
print("case = " + str(x) + " cost = " + str(cost))
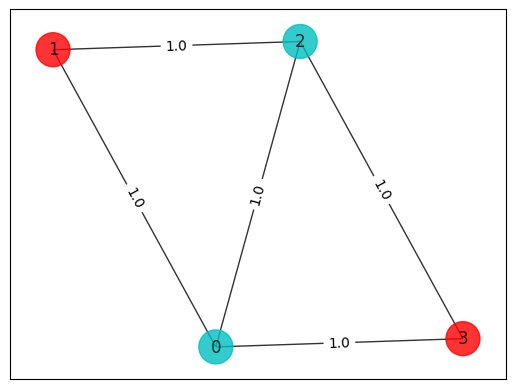
colors = ["r" if xbest_brute[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)
print("\nBest solution = " + str(xbest_brute) + " cost = " + str(best_cost_brute))
case = [0, 0, 0, 0] cost = 0.0
case = [1, 0, 0, 0] cost = 3.0
case = [0, 1, 0, 0] cost = 2.0
case = [1, 1, 0, 0] cost = 3.0
case = [0, 0, 1, 0] cost = 3.0
case = [1, 0, 1, 0] cost = 4.0
case = [0, 1, 1, 0] cost = 3.0
case = [1, 1, 1, 0] cost = 2.0
case = [0, 0, 0, 1] cost = 2.0
case = [1, 0, 0, 1] cost = 3.0
case = [0, 1, 0, 1] cost = 4.0
case = [1, 1, 0, 1] cost = 3.0
case = [0, 0, 1, 1] cost = 3.0
case = [1, 0, 1, 1] cost = 2.0
case = [0, 1, 1, 1] cost = 3.0
case = [1, 1, 1, 1] cost = 0.0
Best solution = [1, 0, 1, 0] cost = 4.0
Mapping to the Ising problem
[6]:
max_cut = Maxcut(w)
qp = max_cut.to_quadratic_program()
print(qp.prettyprint())
Problem name: Max-cut
Maximize
-2*x_0*x_1 - 2*x_0*x_2 - 2*x_0*x_3 - 2*x_1*x_2 - 2*x_2*x_3 + 3*x_0 + 2*x_1
+ 3*x_2 + 2*x_3
Subject to
No constraints
Binary variables (4)
x_0 x_1 x_2 x_3
[7]:
qubitOp, offset = qp.to_ising()
print("Offset:", offset)
print("Ising Hamiltonian:")
print(str(qubitOp))
Offset: -2.5
Ising Hamiltonian:
SparsePauliOp(['IIZZ', 'IZIZ', 'ZIIZ', 'IZZI', 'ZZII'],
coeffs=[0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j])
[8]:
# solving Quadratic Program using exact classical eigensolver
exact = MinimumEigenOptimizer(NumPyMinimumEigensolver())
result = exact.solve(qp)
print(result.prettyprint())
objective function value: 4.0
variable values: x_0=1.0, x_1=0.0, x_2=1.0, x_3=0.0
status: SUCCESS
Checking that the full Hamiltonian gives the right cost
[9]:
# Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver()
result = ee.compute_minimum_eigenvalue(qubitOp)
x = max_cut.sample_most_likely(result.eigenstate)
print("energy:", result.eigenvalue.real)
print("max-cut objective:", result.eigenvalue.real + offset)
print("solution:", x)
print("solution objective:", qp.objective.evaluate(x))
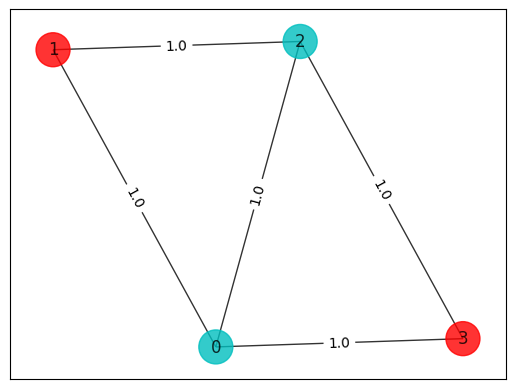
colors = ["r" if x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)
energy: -1.5
max-cut objective: -4.0
solution: [1. 0. 1. 0.]
solution objective: 4.0
Running it on quantum computer
[10]:
algorithm_globals.random_seed = 123
seed = 10598
[11]:
# construct SamplingVQE
optimizer = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, "ry", "cz", reps=5, entanglement="linear")
vqe = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=optimizer)
# run SamplingVQE
result = vqe.compute_minimum_eigenvalue(qubitOp)
# print results
x = max_cut.sample_most_likely(result.eigenstate)
print("energy:", result.eigenvalue.real)
print("time:", result.optimizer_time)
print("max-cut objective:", result.eigenvalue.real + offset)
print("solution:", x)
print("solution objective:", qp.objective.evaluate(x))
# plot results
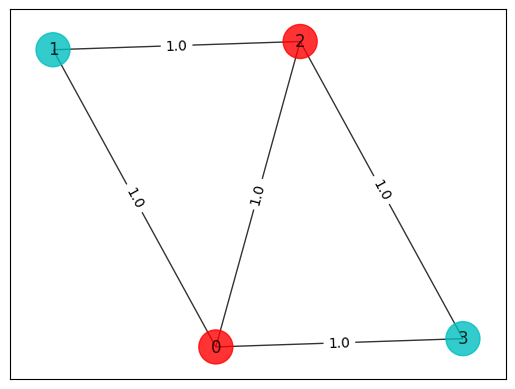
colors = ["r" if x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)
energy: -1.5
time: 17.79062008857727
max-cut objective: -4.0
solution: [0 1 0 1]
solution objective: 4.0
[12]:
# create minimum eigen optimizer based on SamplingVQE
vqe_optimizer = MinimumEigenOptimizer(vqe)
# solve quadratic program
result = vqe_optimizer.solve(qp)
print(result.prettyprint())
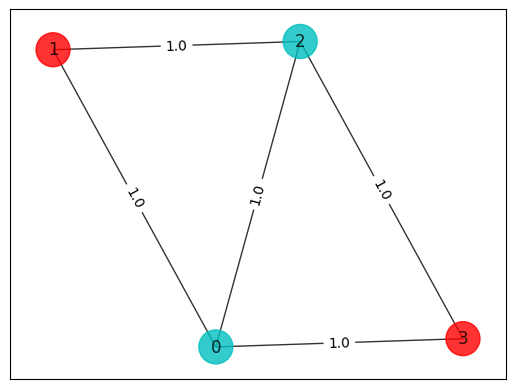
colors = ["r" if result.x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)
objective function value: 4.0
variable values: x_0=1.0, x_1=0.0, x_2=1.0, x_3=0.0
status: SUCCESS
Traveling Salesman Problem
[13]:
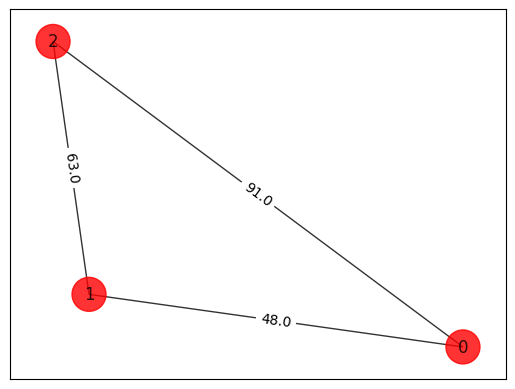
# Generating a graph of 3 nodes
n = 3
num_qubits = n**2
tsp = Tsp.create_random_instance(n, seed=123)
adj_matrix = nx.to_numpy_array(tsp.graph)
print("distance\n", adj_matrix)
colors = ["r" for node in tsp.graph.nodes]
pos = [tsp.graph.nodes[node]["pos"] for node in tsp.graph.nodes]
draw_graph(tsp.graph, colors, pos)
distance
[[ 0. 48. 91.]
[48. 0. 63.]
[91. 63. 0.]]
Brute force approach
[14]:
from itertools import permutations
def brute_force_tsp(w, N):
a = list(permutations(range(1, N)))
last_best_distance = 1e10
for i in a:
distance = 0
pre_j = 0
for j in i:
distance = distance + w[j, pre_j]
pre_j = j
distance = distance + w[pre_j, 0]
order = (0,) + i
if distance < last_best_distance:
best_order = order
last_best_distance = distance
print("order = " + str(order) + " Distance = " + str(distance))
return last_best_distance, best_order
best_distance, best_order = brute_force_tsp(adj_matrix, n)
print(
"Best order from brute force = "
+ str(best_order)
+ " with total distance = "
+ str(best_distance)
)
def draw_tsp_solution(G, order, colors, pos):
G2 = nx.DiGraph()
G2.add_nodes_from(G)
n = len(order)
for i in range(n):
j = (i + 1) % n
G2.add_edge(order[i], order[j], weight=G[order[i]][order[j]]["weight"])
default_axes = plt.axes(frameon=True)
nx.draw_networkx(
G2, node_color=colors, edge_color="b", node_size=600, alpha=0.8, ax=default_axes, pos=pos
)
edge_labels = nx.get_edge_attributes(G2, "weight")
nx.draw_networkx_edge_labels(G2, pos, font_color="b", edge_labels=edge_labels)
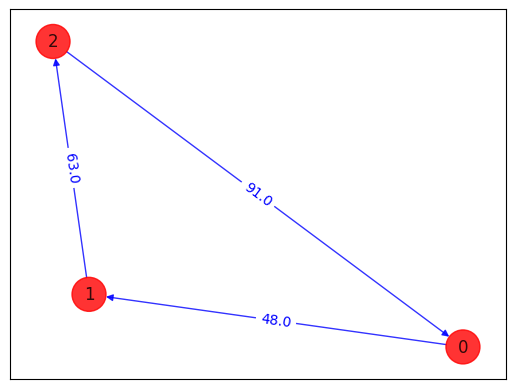
draw_tsp_solution(tsp.graph, best_order, colors, pos)
order = (0, 1, 2) Distance = 202.0
Best order from brute force = (0, 1, 2) with total distance = 202.0
Mapping to the Ising problem
[15]:
qp = tsp.to_quadratic_program()
print(qp.prettyprint())
Problem name: TSP
Minimize
48*x_0_0*x_1_1 + 48*x_0_0*x_1_2 + 91*x_0_0*x_2_1 + 91*x_0_0*x_2_2
+ 48*x_0_1*x_1_0 + 48*x_0_1*x_1_2 + 91*x_0_1*x_2_0 + 91*x_0_1*x_2_2
+ 48*x_0_2*x_1_0 + 48*x_0_2*x_1_1 + 91*x_0_2*x_2_0 + 91*x_0_2*x_2_1
+ 63*x_1_0*x_2_1 + 63*x_1_0*x_2_2 + 63*x_1_1*x_2_0 + 63*x_1_1*x_2_2
+ 63*x_1_2*x_2_0 + 63*x_1_2*x_2_1
Subject to
Linear constraints (6)
x_0_0 + x_0_1 + x_0_2 == 1 'c0'
x_1_0 + x_1_1 + x_1_2 == 1 'c1'
x_2_0 + x_2_1 + x_2_2 == 1 'c2'
x_0_0 + x_1_0 + x_2_0 == 1 'c3'
x_0_1 + x_1_1 + x_2_1 == 1 'c4'
x_0_2 + x_1_2 + x_2_2 == 1 'c5'
Binary variables (9)
x_0_0 x_0_1 x_0_2 x_1_0 x_1_1 x_1_2 x_2_0 x_2_1 x_2_2
[16]:
from qiskit_optimization.converters import QuadraticProgramToQubo
qp2qubo = QuadraticProgramToQubo()
qubo = qp2qubo.convert(qp)
qubitOp, offset = qubo.to_ising()
print("Offset:", offset)
print("Ising Hamiltonian:")
print(str(qubitOp))
Offset: 7581.0
Ising Hamiltonian:
SparsePauliOp(['IIIIIIIIZ', 'IIIIIIIZI', 'IIIIIIZII', 'IIIIIZIII', 'IIIIZIIII', 'IIIZIIIII', 'IIZIIIIII', 'IZIIIIIII', 'ZIIIIIIII', 'IIIIIIIZZ', 'IIIIIIZIZ', 'IIIIIZIIZ', 'IIIIZIIIZ', 'IIIZIIIIZ', 'IIZIIIIIZ', 'IZIIIIIIZ', 'ZIIIIIIIZ', 'IIIIIIZZI', 'IIIIIZIZI', 'IIIIZIIZI', 'IIIZIIIZI', 'IIZIIIIZI', 'IZIIIIIZI', 'ZIIIIIIZI', 'IIIIIZZII', 'IIIIZIZII', 'IIIZIIZII', 'IIZIIIZII', 'IZIIIIZII', 'ZIIIIIZII', 'IIIIZZIII', 'IIIZIZIII', 'IIZIIZIII', 'IZIIIZIII', 'ZIIIIZIII', 'IIIZZIIII', 'IIZIZIIII', 'IZIIZIIII', 'ZIIIZIIII', 'IIZZIIIII', 'IZIZIIIII', 'ZIIZIIIII', 'IZZIIIIII', 'ZIZIIIIII', 'ZZIIIIIII'],
coeffs=[-1282.5 +0.j, -1282.5 +0.j, -1282.5 +0.j, -1268.5 +0.j, -1268.5 +0.j,
-1268.5 +0.j, -1290. +0.j, -1290. +0.j, -1290. +0.j, 606.5 +0.j,
606.5 +0.j, 606.5 +0.j, 12. +0.j, 12. +0.j, 606.5 +0.j,
22.75+0.j, 22.75+0.j, 606.5 +0.j, 12. +0.j, 606.5 +0.j,
12. +0.j, 22.75+0.j, 606.5 +0.j, 22.75+0.j, 12. +0.j,
12. +0.j, 606.5 +0.j, 22.75+0.j, 22.75+0.j, 606.5 +0.j,
606.5 +0.j, 606.5 +0.j, 606.5 +0.j, 15.75+0.j, 15.75+0.j,
606.5 +0.j, 15.75+0.j, 606.5 +0.j, 15.75+0.j, 15.75+0.j,
15.75+0.j, 606.5 +0.j, 606.5 +0.j, 606.5 +0.j, 606.5 +0.j])
[17]:
result = exact.solve(qubo)
print(result.prettyprint())
objective function value: 202.0
variable values: x_0_0=1.0, x_0_1=0.0, x_0_2=0.0, x_1_0=0.0, x_1_1=1.0, x_1_2=0.0, x_2_0=0.0, x_2_1=0.0, x_2_2=1.0
status: SUCCESS
[18]:
# Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver()
result = ee.compute_minimum_eigenvalue(qubitOp)
print("energy:", result.eigenvalue.real)
print("tsp objective:", result.eigenvalue.real + offset)
x = tsp.sample_most_likely(result.eigenstate)
print("feasible:", qubo.is_feasible(x))
z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
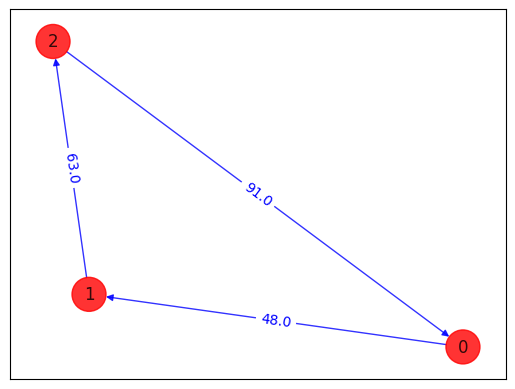
draw_tsp_solution(tsp.graph, z, colors, pos)
energy: -7379.0
tsp objective: 202.0
feasible: True
solution: [0, 1, 2]
solution objective: 202.0
Running it on quantum computer
[19]:
algorithm_globals.random_seed = 123
seed = 10598
[20]:
optimizer = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, "ry", "cz", reps=5, entanglement="linear")
vqe = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=optimizer)
result = vqe.compute_minimum_eigenvalue(qubitOp)
print("energy:", result.eigenvalue.real)
print("time:", result.optimizer_time)
x = tsp.sample_most_likely(result.eigenstate)
print("feasible:", qubo.is_feasible(x))
z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
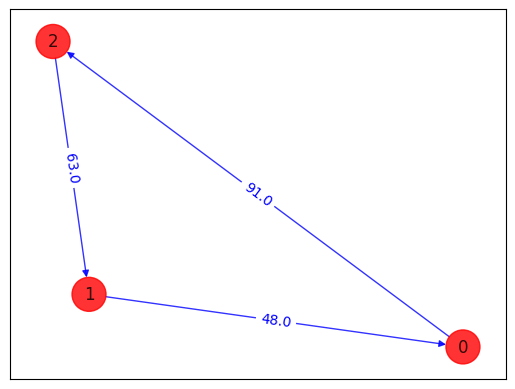
draw_tsp_solution(tsp.graph, z, colors, pos)
energy: -7154.7705078125
time: 46.16239619255066
feasible: True
solution: [1, 0, 2]
solution objective: 202.0
[21]:
algorithm_globals.random_seed = 123
seed = 10598
[22]:
# create minimum eigen optimizer based on SamplingVQE
vqe_optimizer = MinimumEigenOptimizer(vqe)
# solve quadratic program
result = vqe_optimizer.solve(qp)
print(result.prettyprint())
z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
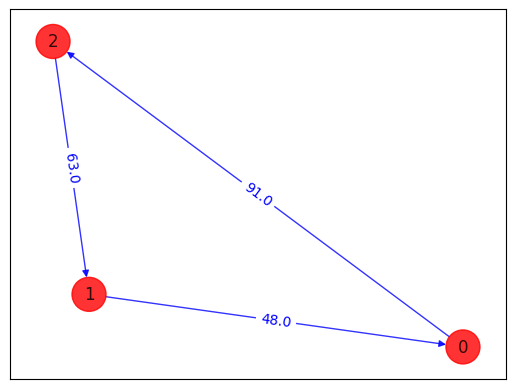
draw_tsp_solution(tsp.graph, z, colors, pos)
objective function value: 202.0
variable values: x_0_0=0.0, x_0_1=0.0, x_0_2=1.0, x_1_0=0.0, x_1_1=1.0, x_1_2=0.0, x_2_0=1.0, x_2_1=0.0, x_2_2=0.0
status: SUCCESS
solution: [1, 0, 2]
solution objective: 202.0
[ ]: