10 - Effective Dimension of Qiskit Neural Networks

# This code is at:
# https://qiskit-community.github.io/qiskit-machine-learning/tutorials/10_effective_dimension.html

# Necessary imports
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit.library import ZFeatureMap, RealAmplitudes
from qiskit_machine_learning.optimizers import COBYLA
from qiskit_machine_learning.utils import algorithm_globals
#from qiskit.primitives import StatevectorSampler as Sampler, StatevectorEstimator as Estimator

from quantumrings.toolkit.qiskit import QrSamplerV1 as Sampler
from quantumrings.toolkit.qiskit import QrEstimatorV1 as Estimator

from sklearn.datasets import make_classification
from sklearn.preprocessing import MinMaxScaler

from qiskit_machine_learning.circuit.library import QNNCircuit
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier
from qiskit_machine_learning.neural_networks import EffectiveDimension, LocalEffectiveDimension
#from qiskit_machine_learning.neural_networks import SamplerQNN, EstimatorQNN

from quantumrings.toolkit.qiskit.machine_learning import QrEstimatorQNN as EstimatorQNN
from quantumrings.toolkit.qiskit.machine_learning import QrSamplerQNN as SamplerQNN

# set random seed
algorithm_globals.random_seed = 42
sampler = Sampler()
estimator = Estimator()

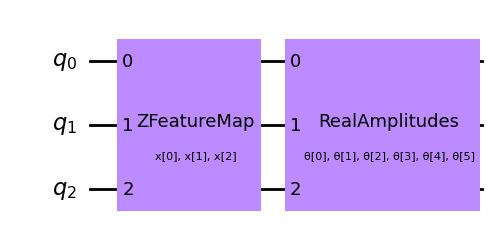
num_qubits = 3
# combine a custom feature map and ansatz into a single circuit
qc = QNNCircuit(
    feature_map=ZFeatureMap(feature_dimension=num_qubits, reps=1),
    ansatz=RealAmplitudes(num_qubits, reps=1),
)
qc.draw(output="mpl", style="clifford")

# parity maps bitstrings to 0 or 1
def parity(x):
    return "{:b}".format(x).count("1") % 2


output_shape = 2  # corresponds to the number of classes, possible outcomes of the (parity) mapping.

# construct QNN
qnn = SamplerQNN(
    circuit=qc,
    interpret=parity,
    output_shape=output_shape,
    sparse=False,
    sampler=sampler,
)

# we can set the total number of input samples and weight samples for random selection
num_input_samples = 10
num_weight_samples = 10

global_ed = EffectiveDimension(
    qnn=qnn, weight_samples=num_weight_samples, input_samples=num_input_samples
)

# we can also provide user-defined samples and parameters
input_samples = algorithm_globals.random.normal(0, 1, size=(10, qnn.num_inputs))
weight_samples = algorithm_globals.random.uniform(0, 1, size=(10, qnn.num_weights))

global_ed = EffectiveDimension(qnn=qnn, weight_samples=weight_samples, input_samples=input_samples)

# finally, we will define ranges to test different numbers of data, n
n = [5000, 8000, 10000, 40000, 60000, 100000, 150000, 200000, 500000, 1000000]

global_eff_dim_0 = global_ed.get_effective_dimension(dataset_size=n[0])

d = qnn.num_weights

print("Data size: {}, global effective dimension: {:.4f}".format(n[0], global_eff_dim_0))
print(
    "Number of weights: {}, normalized effective dimension: {:.4f}".format(d, global_eff_dim_0 / d)
)

Data size: 5000, global effective dimension: 4.6996
Number of weights: 6, normalized effective dimension: 0.7833

global_eff_dim_1 = global_ed.get_effective_dimension(dataset_size=n)

print("Effective dimension: {}".format(global_eff_dim_1))
print("Number of weights: {}".format(d))

Effective dimension: [4.70355082 4.75259529 4.77756039 4.94077118 4.98729723 5.04323376
 5.08507613 5.11328317 5.19484127 5.24859738]
Number of weights: 6

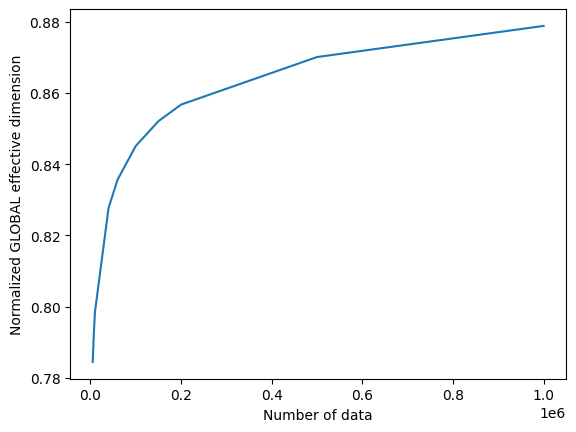
# plot the normalized effective dimension for the model
plt.plot(n, np.array(global_eff_dim_1) / d)
plt.xlabel("Number of data")
plt.ylabel("Normalized GLOBAL effective dimension")
plt.show()

num_inputs = 3
num_samples = 50

X, y = make_classification(
    n_samples=num_samples,
    n_features=num_inputs,
    n_informative=3,
    n_redundant=0,
    n_clusters_per_class=1,
    class_sep=2.0,
)
X = MinMaxScaler().fit_transform(X)
y = 2 * y - 1  # labels in {-1, 1}

estimator_qnn = EstimatorQNN(circuit=qc, estimator=estimator)

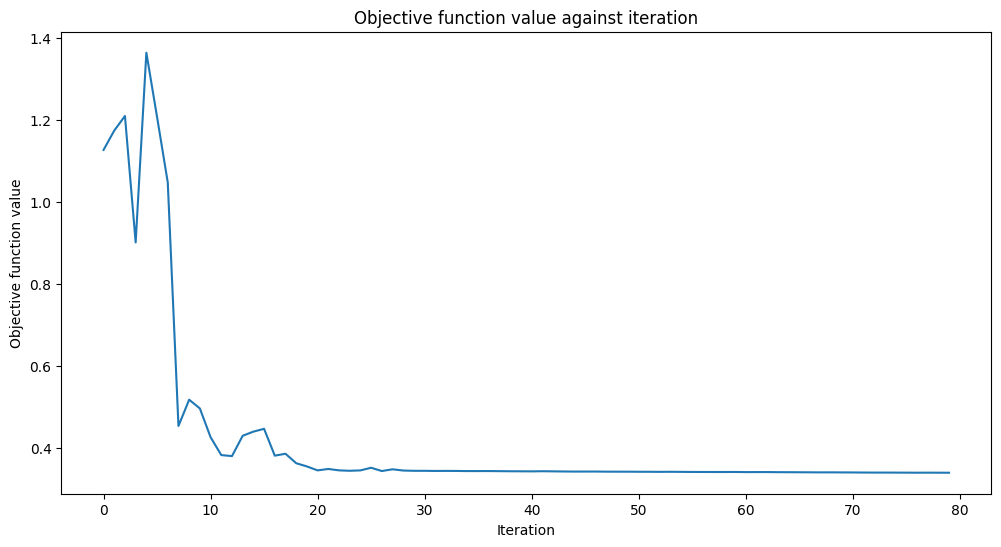
# callback function that draws a live plot when the .fit() method is called
def callback_graph(weights, obj_func_eval):
    clear_output(wait=True)
    objective_func_vals.append(obj_func_eval)
    plt.title("Objective function value against iteration")
    plt.xlabel("Iteration")
    plt.ylabel("Objective function value")
    plt.plot(range(len(objective_func_vals)), objective_func_vals)
    plt.show()

# construct classifier
initial_point = algorithm_globals.random.random(estimator_qnn.num_weights)

estimator_classifier = NeuralNetworkClassifier(
    neural_network=estimator_qnn,
    optimizer=COBYLA(maxiter=80),
    initial_point=initial_point,
    callback=callback_graph,
)

# create empty array for callback to store evaluations of the objective function (callback)
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)

# fit classifier to data
estimator_classifier.fit(X, y)

# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)

# score classifier
estimator_classifier.score(X, y)

0.98

trained_weights = estimator_classifier.weights

# get Local Effective Dimension for set of trained weights
local_ed_trained = LocalEffectiveDimension(
    qnn=estimator_qnn, weight_samples=trained_weights, input_samples=X
)

local_eff_dim_trained = local_ed_trained.get_effective_dimension(dataset_size=n)

print(
    "normalized local effective dimensions for trained QNN: ",
    local_eff_dim_trained / estimator_qnn.num_weights,
)

normalized local effective dimensions for trained QNN:  [0.45239996 0.45512006 0.45653915 0.46649174 0.46983293 0.4744932
 0.47865471 0.4819014  0.49406545 0.50511606]

# get Local Effective Dimension for set of untrained weights
local_ed_untrained = LocalEffectiveDimension(
    qnn=estimator_qnn, weight_samples=initial_point, input_samples=X
)

local_eff_dim_untrained = local_ed_untrained.get_effective_dimension(dataset_size=n)

print(
    "normalized local effective dimensions for untrained QNN: ",
    local_eff_dim_untrained / estimator_qnn.num_weights,
)

normalized local effective dimensions for untrained QNN:  [0.67352588 0.68553608 0.69150978 0.73017426 0.74137833 0.75503966
 0.76539332 0.77243218 0.79300413 0.8066959 ]

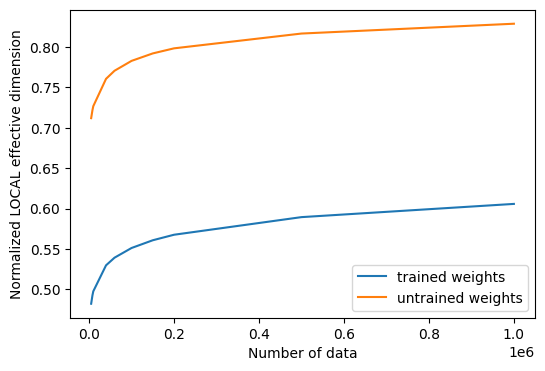
# plot the normalized effective dimension for the model
plt.plot(n, np.array(local_eff_dim_trained) / estimator_qnn.num_weights, label="trained weights")
plt.plot(
    n, np.array(local_eff_dim_untrained) / estimator_qnn.num_weights, label="untrained weights"
)

plt.xlabel("Number of data")
plt.ylabel("Normalized LOCAL effective dimension")
plt.legend()
plt.show()