10 - Warm-starting quantum optimization

# This code is from the tutorial at:
# https://qiskit-community.github.io/qiskit-optimization/tutorials/10_warm_start_qaoa.html

import numpy as np
import copy

# Problem modelling imports
from docplex.mp.model import Model

# Qiskit imports
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals

# Switch to Quantum Rings's Sampler
#from qiskit.primitives import Sampler
from quantumrings.toolkit.qiskit import QrSamplerV1 as Sampler

from qiskit_optimization.algorithms import MinimumEigenOptimizer, CplexOptimizer
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.problems.variable import VarType
from qiskit_optimization.converters.quadratic_program_to_qubo import QuadraticProgramToQubo
from qiskit_optimization.translators import from_docplex_mp

Preliminaries: relaxing QUBOs

def create_problem(mu: np.array, sigma: np.array, total: int = 3) -> QuadraticProgram:
    """Solve the quadratic program using docplex."""

    mdl = Model()
    x = [mdl.binary_var("x%s" % i) for i in range(len(sigma))]

    objective = mdl.sum([mu[i] * x[i] for i in range(len(mu))])
    objective -= 2 * mdl.sum(
        [sigma[i, j] * x[i] * x[j] for i in range(len(mu)) for j in range(len(mu))]
    )
    mdl.maximize(objective)
    cost = mdl.sum(x)
    mdl.add_constraint(cost == total)

    qp = from_docplex_mp(mdl)
    return qp


def relax_problem(problem) -> QuadraticProgram:
    """Change all variables to continuous."""
    relaxed_problem = copy.deepcopy(problem)
    for variable in relaxed_problem.variables:
        variable.vartype = VarType.CONTINUOUS

    return relaxed_problem

mu = np.array([3.418, 2.0913, 6.2415, 4.4436, 10.892, 3.4051])
sigma = np.array(
    [
        [1.07978412, 0.00768914, 0.11227606, -0.06842969, -0.01016793, -0.00839765],
        [0.00768914, 0.10922887, -0.03043424, -0.0020045, 0.00670929, 0.0147937],
        [0.11227606, -0.03043424, 0.985353, 0.02307313, -0.05249785, 0.00904119],
        [-0.06842969, -0.0020045, 0.02307313, 0.6043817, 0.03740115, -0.00945322],
        [-0.01016793, 0.00670929, -0.05249785, 0.03740115, 0.79839634, 0.07616951],
        [-0.00839765, 0.0147937, 0.00904119, -0.00945322, 0.07616951, 1.08464544],
    ]
)

qubo = create_problem(mu, sigma)
print(qubo.prettyprint())

Problem name: docplex_model1

Maximize
  -2.15956824*x0^2 - 0.03075656*x0*x1 - 0.44910424*x0*x2 + 0.27371876*x0*x3
  + 0.04067172*x0*x4 + 0.0335906*x0*x5 - 0.21845774*x1^2 + 0.12173696*x1*x2
  + 0.008018*x1*x3 - 0.02683716*x1*x4 - 0.0591748*x1*x5 - 1.970706*x2^2
  - 0.09229252*x2*x3 + 0.2099914*x2*x4 - 0.03616476*x2*x5 - 1.2087634*x3^2
  - 0.1496046*x3*x4 + 0.03781288*x3*x5 - 1.59679268*x4^2 - 0.30467804*x4*x5
  - 2.16929088*x5^2 + 3.418*x0 + 2.0913*x1 + 6.2415*x2 + 4.4436*x3 + 10.892*x4
  + 3.4051*x5

Subject to
  Linear constraints (1)
    x0 + x1 + x2 + x3 + x4 + x5 == 3  'c0'

  Binary variables (6)
    x0 x1 x2 x3 x4 x5

result = CplexOptimizer().solve(qubo)
print(result.prettyprint())

objective function value: 16.7689322
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

qp = relax_problem(QuadraticProgramToQubo().convert(qubo))
print(qp.prettyprint())

Problem name: docplex_model1

Minimize
  44.84880018*x0^2 + 85.40922044*x0*x1 + 85.82756812*x0*x2
  + 85.10474511999999*x0*x3 + 85.33779215999999*x0*x4 + 85.34487328*x0*x5
  + 42.90768968*x1^2 + 85.25672692*x1*x2 + 85.37044588*x1*x3 + 85.40530104*x1*x4
  + 85.43763867999999*x1*x5 + 44.65993794*x2^2 + 85.4707564*x2*x3
  + 85.16847247999999*x2*x4 + 85.41462863999999*x2*x5 + 43.89799534*x3^2
  + 85.52806848*x3*x4 + 85.34065100000001*x3*x5 + 44.28602462*x4^2
  + 85.68314192*x4*x5 + 44.85852282*x5^2 - 259.55339164*x0
  - 258.22669163999996*x1 - 262.37689163999994*x2 - 260.57899163999997*x3
  - 267.02739163999996*x4 - 259.54049163999997*x5 + 384.20308746

Subject to
  No constraints

  Continuous variables (6)
    0 <= x0 <= 1
    0 <= x1 <= 1
    0 <= x2 <= 1
    0 <= x3 <= 1
    0 <= x4 <= 1
    0 <= x5 <= 1

sol = CplexOptimizer().solve(qp)
print(sol.prettyprint())

objective function value: -17.01205502568274
variable values: x0=0.17524995761801201, x1=1.4803888163984595e-07, x2=0.9709053264087679, x3=0.7384168677494151, x4=0.9999999916475085, x5=0.14438904470168346
status: SUCCESS

c_stars = sol.samples[0].x
print(c_stars)

[0.17524995761801201, 1.4803888163984595e-07, 0.9709053264087679, 0.7384168677494151, 0.9999999916475085, 0.14438904470168346]

QAOA

algorithm_globals.random_seed = 12345
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
exact_mes = NumPyMinimumEigensolver()

qaoa = MinimumEigenOptimizer(qaoa_mes)

qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())

objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

from qiskit import QuantumCircuit

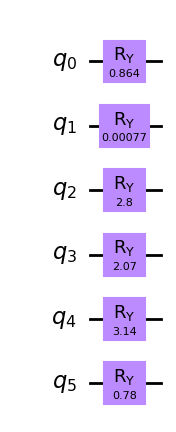
thetas = [2 * np.arcsin(np.sqrt(c_star)) for c_star in c_stars]

init_qc = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
    init_qc.ry(theta, idx)

init_qc.draw(output="mpl", style="clifford")

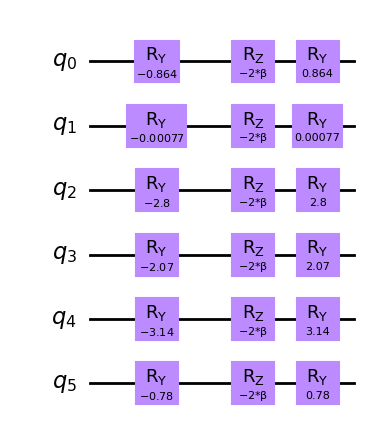
from qiskit.circuit import Parameter

beta = Parameter("β")

ws_mixer = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
    ws_mixer.ry(-theta, idx)
    ws_mixer.rz(-2 * beta, idx)
    ws_mixer.ry(theta, idx)

ws_mixer.draw(output="mpl", style="clifford")

ws_qaoa_mes = QAOA(
    sampler=Sampler(),
    optimizer=COBYLA(),
    initial_state=init_qc,
    mixer=ws_mixer,
    initial_point=[0.0, 1.0],
)

ws_qaoa = MinimumEigenOptimizer(ws_qaoa_mes)

ws_qaoa_result = ws_qaoa.solve(qubo)
print(ws_qaoa_result.prettyprint())

objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

Analysis

def format_qaoa_samples(samples, max_len: int = 10):
    qaoa_res = []
    for s in samples:
        if sum(s.x) == 3:
            qaoa_res.append(("".join([str(int(_)) for _ in s.x]), s.fval, s.probability))

    res = sorted(qaoa_res, key=lambda x: -x[1])[0:max_len]

    return [(_[0] + f": value: {_[1]:.3f}, probability: {1e2*_[2]:.1f}%") for _ in res]


format_qaoa_samples(qaoa_result.samples)

['001110: value: 16.769, probability: 13.2%',
 '011010: value: 15.744, probability: 3.6%',
 '001011: value: 14.671, probability: 3.1%',
 '101010: value: 14.626, probability: 4.7%',
 '010110: value: 14.234, probability: 2.2%',
 '100110: value: 13.953, probability: 3.7%',
 '000111: value: 13.349, probability: 2.1%',
 '110010: value: 12.410, probability: 0.9%',
 '010011: value: 12.013, probability: 0.8%',
 '100011: value: 11.559, probability: 0.5%']

format_qaoa_samples(ws_qaoa_result.samples)

['001110: value: 16.769, probability: 64.7%',
 '001011: value: 14.671, probability: 1.2%',
 '101010: value: 14.626, probability: 2.5%',
 '100110: value: 13.953, probability: 0.4%',
 '000111: value: 13.349, probability: 0.1%']

Warm-start QAOA

from qiskit_optimization.algorithms import WarmStartQAOAOptimizer

qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
ws_qaoa = WarmStartQAOAOptimizer(
    pre_solver=CplexOptimizer(), relax_for_pre_solver=True, qaoa=qaoa_mes, epsilon=0.0
)

ws_result = ws_qaoa.solve(qubo)
print(ws_result.prettyprint())

objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

format_qaoa_samples(ws_result.samples)

['001110: value: 16.769, probability: 85.3%',
 '001011: value: 14.671, probability: 1.1%',
 '101010: value: 14.626, probability: 0.1%',
 '100110: value: 13.953, probability: 0.5%',
 '000111: value: 13.349, probability: 0.1%']