12 - The Quantum Autoencoder
[1]:
# This code is at:
# https://qiskit-community.github.io/qiskit-machine-learning/tutorials/12_quantum_autoencoder.html
[2]:
import json
import time
import warnings
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import ClassicalRegister, QuantumRegister
from qiskit import QuantumCircuit
from qiskit.circuit.library import RealAmplitudes
#from qiskit.primitives import StatevectorSampler as Sampler
#from qiskit.quantum_info import Statevector
from quantumrings.toolkit.qiskit import QrSamplerV1 as Sampler
from quantumrings.toolkit.qiskit import QrStatevector as Statevector
from qiskit_machine_learning.optimizers import COBYLA
from qiskit_machine_learning.utils import algorithm_globals
from qiskit_machine_learning.circuit.library import RawFeatureVector
#from qiskit_machine_learning.neural_networks import SamplerQNN
from quantumrings.toolkit.qiskit.machine_learning import QrSamplerQNN as SamplerQNN
algorithm_globals.random_seed = 42
sampler = Sampler()
[3]:
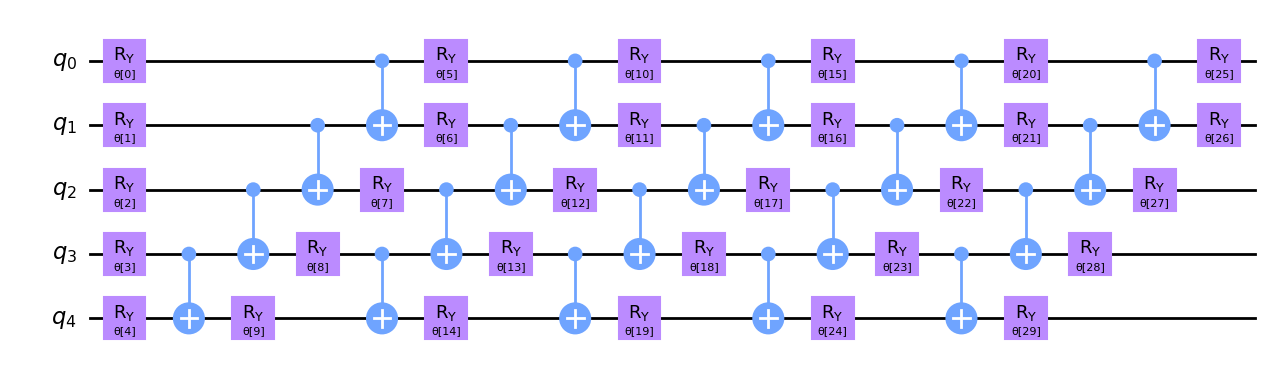
def ansatz(num_qubits):
return RealAmplitudes(num_qubits, reps=5)
[4]:
num_qubits = 5
circ = ansatz(num_qubits)
circ.decompose().draw(output="mpl", style="clifford")
[4]:
[5]:
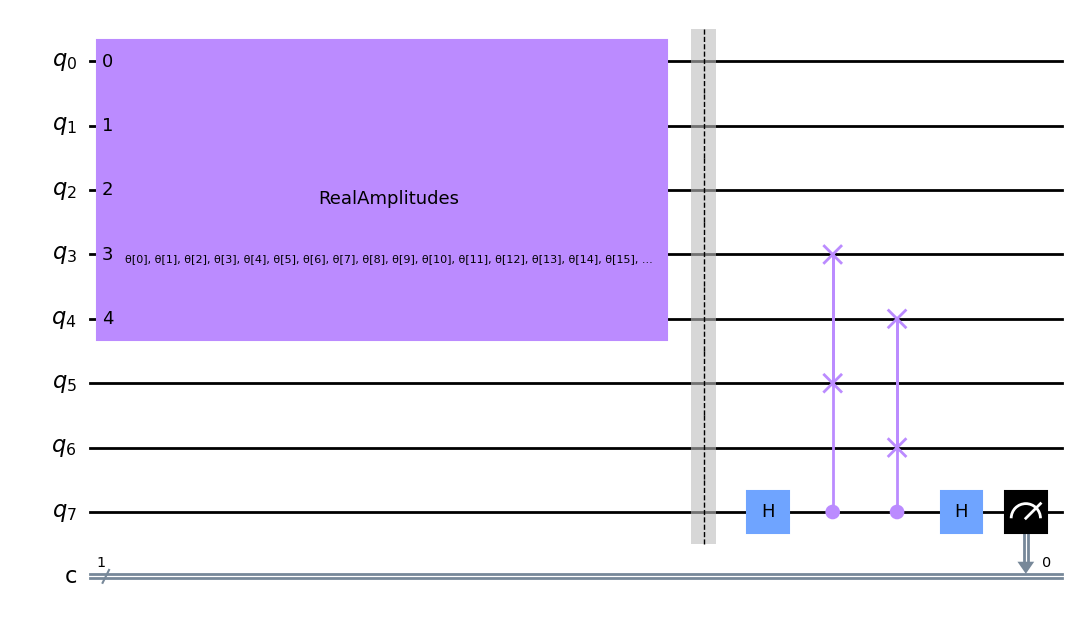
def auto_encoder_circuit(num_latent, num_trash):
qr = QuantumRegister(num_latent + 2 * num_trash + 1, "q")
cr = ClassicalRegister(1, "c")
circuit = QuantumCircuit(qr, cr)
circuit.compose(ansatz(num_latent + num_trash), range(0, num_latent + num_trash), inplace=True)
circuit.barrier()
auxiliary_qubit = num_latent + 2 * num_trash
# swap test
circuit.h(auxiliary_qubit)
for i in range(num_trash):
circuit.cswap(auxiliary_qubit, num_latent + i, num_latent + num_trash + i)
circuit.h(auxiliary_qubit)
circuit.measure(auxiliary_qubit, cr[0])
return circuit
num_latent = 3
num_trash = 2
circuit = auto_encoder_circuit(num_latent, num_trash)
circuit.draw(output="mpl", style="clifford")
[5]:
[6]:
def domain_wall(circuit, a, b):
# Here we place the Domain Wall to qubits a - b in our circuit
for i in np.arange(int(b / 2), int(b)):
circuit.x(i)
return circuit
domain_wall_circuit = domain_wall(QuantumCircuit(5), 0, 5)
domain_wall_circuit.draw("mpl", style="clifford")
[6]:
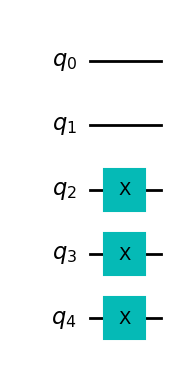
[7]:
ae = auto_encoder_circuit(num_latent, num_trash)
qc = QuantumCircuit(num_latent + 2 * num_trash + 1, 1)
qc = qc.compose(domain_wall_circuit, range(num_latent + num_trash))
qc = qc.compose(ae)
qc.draw(output="mpl", style="clifford")
[7]:

[8]:
# Here we define our interpret for our SamplerQNN
def identity_interpret(x):
return x
qnn = SamplerQNN(
circuit=qc,
input_params=[],
weight_params=ae.parameters,
interpret=identity_interpret,
output_shape=2,
sampler=sampler,
)
[9]:
def cost_func_domain(params_values):
probabilities = qnn.forward([], params_values)
# we pick a probability of getting 1 as the output of the network
cost = np.sum(probabilities[:, 1])
# plotting part
clear_output(wait=True)
objective_func_vals.append(cost)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
return cost
[10]:
opt = COBYLA(maxiter=150)
initial_point = algorithm_globals.random.random(ae.num_parameters)
objective_func_vals = []
# make the plot nicer
plt.rcParams["figure.figsize"] = (12, 6)
start = time.time()
opt_result = opt.minimize(cost_func_domain, initial_point)
elapsed = time.time() - start
print(f"Fit in {elapsed:0.2f} seconds")
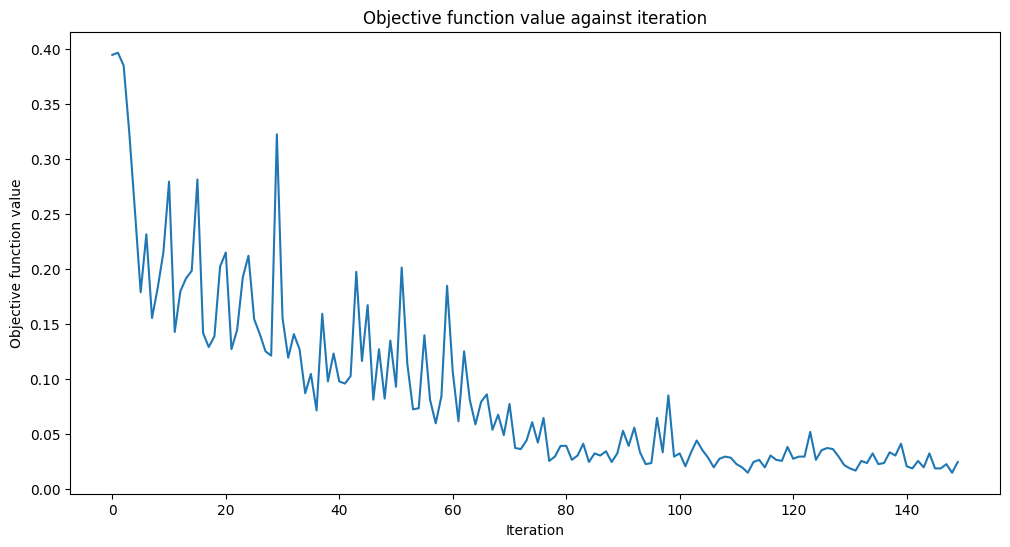
Fit in 64.06 seconds
[11]:
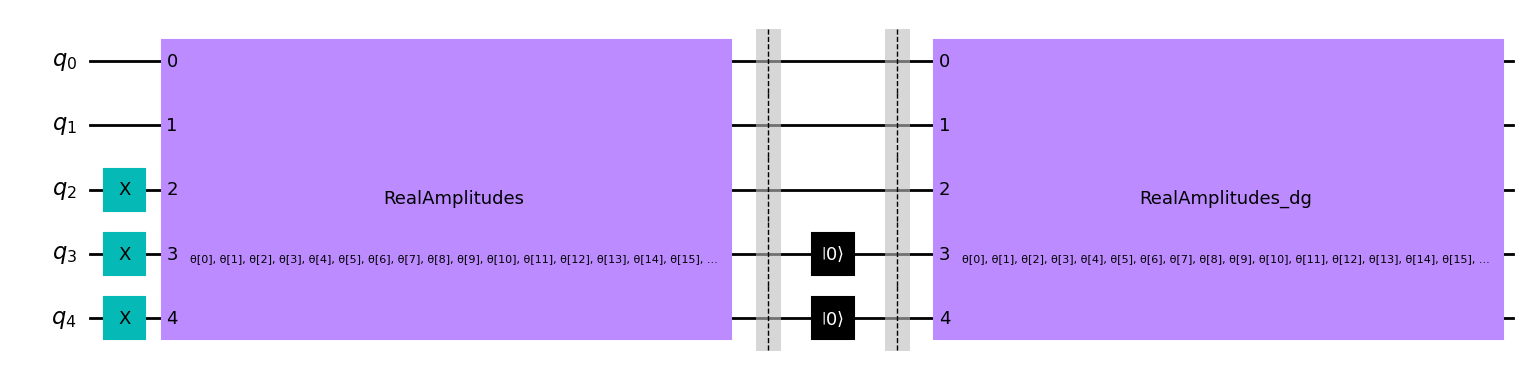
test_qc = QuantumCircuit(num_latent + num_trash)
test_qc = test_qc.compose(domain_wall_circuit)
ansatz_qc = ansatz(num_latent + num_trash)
test_qc = test_qc.compose(ansatz_qc)
test_qc.barrier()
test_qc.reset(4)
test_qc.reset(3)
test_qc.barrier()
test_qc = test_qc.compose(ansatz_qc.inverse())
test_qc.draw(output="mpl", style="clifford")
[11]:
[12]:
test_qc = test_qc.assign_parameters(opt_result.x)
[13]:
domain_wall_state = Statevector(domain_wall_circuit).data
output_state = Statevector(test_qc).data
fidelity = np.sqrt(np.dot(domain_wall_state.conj(), output_state) ** 2)
print("Fidelity of our Output State with our Input State: ", fidelity.real)
Fidelity of our Output State with our Input State: 0.9907927412447166
[14]:
def zero_idx(j, i):
# Index for zero pixels
return [
[i, j],
[i - 1, j - 1],
[i - 1, j + 1],
[i - 2, j - 1],
[i - 2, j + 1],
[i - 3, j - 1],
[i - 3, j + 1],
[i - 4, j - 1],
[i - 4, j + 1],
[i - 5, j],
]
def one_idx(i, j):
# Index for one pixels
return [[i, j - 1], [i, j - 2], [i, j - 3], [i, j - 4], [i, j - 5], [i - 1, j - 4], [i, j]]
def get_dataset_digits(num, draw=True):
# Create Dataset containing zero and one
train_images = []
train_labels = []
for i in range(int(num / 2)):
# First we introduce background noise
empty = np.array([algorithm_globals.random.uniform(0, 0.1) for i in range(32)]).reshape(
8, 4
)
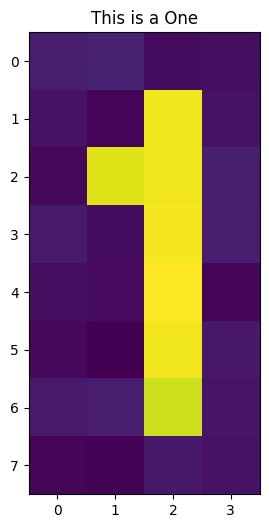
# Now we insert the pixels for the one
for i, j in one_idx(2, 6):
empty[j][i] = algorithm_globals.random.uniform(0.9, 1)
train_images.append(empty)
train_labels.append(1)
if draw:
plt.title("This is a One")
plt.imshow(train_images[-1])
plt.show()
for i in range(int(num / 2)):
empty = np.array([algorithm_globals.random.uniform(0, 0.1) for i in range(32)]).reshape(
8, 4
)
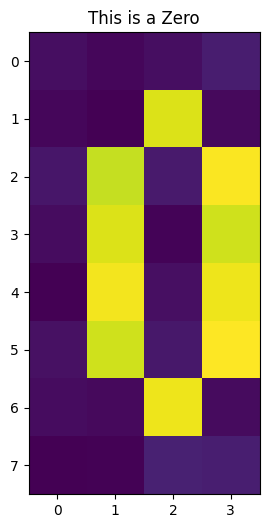
# Now we insert the pixels for the zero
for k, j in zero_idx(2, 6):
empty[k][j] = algorithm_globals.random.uniform(0.9, 1)
train_images.append(empty)
train_labels.append(0)
if draw:
plt.imshow(train_images[-1])
plt.title("This is a Zero")
plt.show()
train_images = np.array(train_images)
train_images = train_images.reshape(len(train_images), 32)
for i in range(len(train_images)):
sum_sq = np.sum(train_images[i] ** 2)
train_images[i] = train_images[i] / np.sqrt(sum_sq)
return train_images, train_labels
train_images, __ = get_dataset_digits(2)
[15]:
num_latent = 3
num_trash = 2
fm = RawFeatureVector(2 ** (num_latent + num_trash))
ae = auto_encoder_circuit(num_latent, num_trash)
qc = QuantumCircuit(num_latent + 2 * num_trash + 1, 1)
qc = qc.compose(fm, range(num_latent + num_trash))
qc = qc.compose(ae)
qc.draw(output="mpl", style="clifford")
[15]:

[16]:
def identity_interpret(x):
return x
qnn = SamplerQNN(
circuit=qc,
input_params=fm.parameters,
weight_params=ae.parameters,
interpret=identity_interpret,
output_shape=2,
sampler=sampler,
)
[17]:
def cost_func_digits(params_values):
probabilities = qnn.forward(train_images, params_values)
cost = np.sum(probabilities[:, 1]) / train_images.shape[0]
# plotting part
clear_output(wait=True)
objective_func_vals.append(cost)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
return cost
[18]:
with open("C:\\Users\\vkasi\\QRForQiskit-MachineLearning\\12_qae_initial_point.json", "r") as f:
initial_point = json.load(f)
[19]:
opt = COBYLA(maxiter=150)
objective_func_vals = []
# make the plot nicer
plt.rcParams["figure.figsize"] = (12, 6)
start = time.time()
opt_result = opt.minimize(fun=cost_func_digits, x0=initial_point)
elapsed = time.time() - start
print(f"Fit in {elapsed:0.2f} seconds")
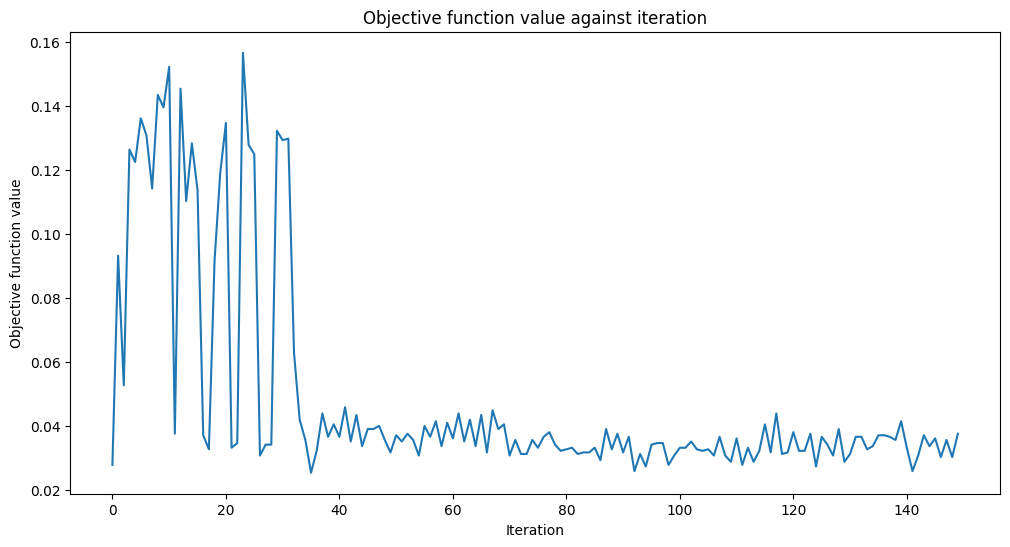
Fit in 709.30 seconds
[20]:
# Test
test_qc = QuantumCircuit(num_latent + num_trash)
test_qc = test_qc.compose(fm)
ansatz_qc = ansatz(num_latent + num_trash)
test_qc = test_qc.compose(ansatz_qc)
test_qc.barrier()
test_qc.reset(4)
test_qc.reset(3)
test_qc.barrier()
test_qc = test_qc.compose(ansatz_qc.inverse())
# sample new images
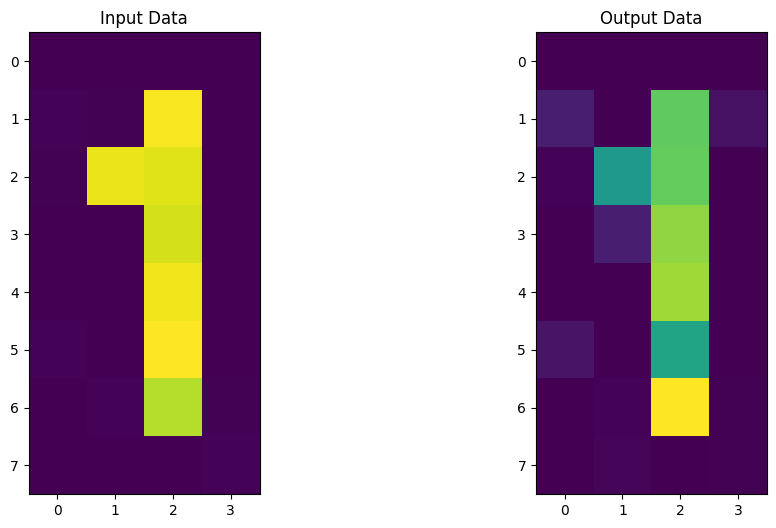
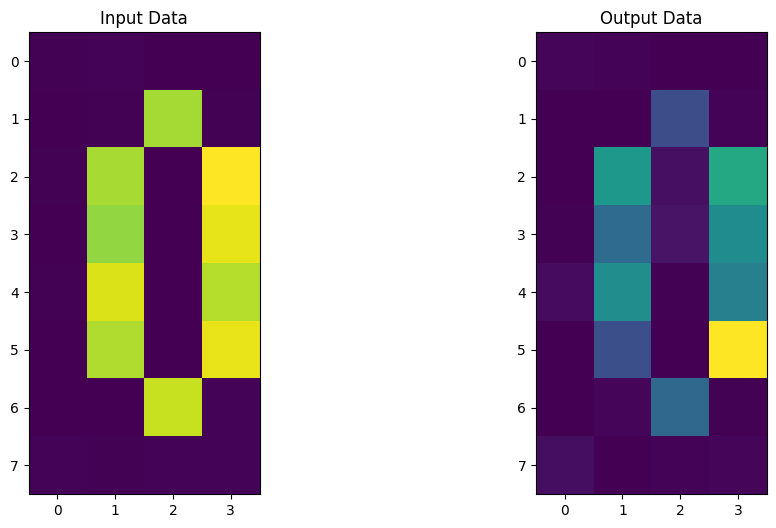
test_images, test_labels = get_dataset_digits(2, draw=False)
for image, label in zip(test_images, test_labels):
original_qc = fm.assign_parameters(image)
original_sv = Statevector(original_qc).data
original_sv = np.reshape(np.abs(original_sv) ** 2, (8, 4))
param_values = np.concatenate((image, opt_result.x))
output_qc = test_qc.assign_parameters(param_values)
output_sv = Statevector(output_qc).data
output_sv = np.reshape(np.abs(output_sv) ** 2, (8, 4))
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(original_sv)
ax1.set_title("Input Data")
ax2.imshow(output_sv)
ax2.set_title("Output Data")
plt.show()
[ ]: