12-Nature Tutorial- Binding Energy
[ ]:
#This code is at
#https://qiskit-community.github.io/qiskit-nature/tutorials/12_deuteron_binding_energy.html
[1]:
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display, clear_output
#from qiskit.primitives import Estimator
from qiskit_algorithms import VQE
from qiskit_algorithms.observables_evaluator import estimate_observables
from qiskit_algorithms.optimizers import COBYLA, SLSQP, SPSA, QNSPSA
from qiskit_algorithms.utils import algorithm_globals
from qiskit.circuit import QuantumCircuit, Parameter
from qiskit.circuit.library import TwoLocal
from qiskit.quantum_info import Pauli, SparsePauliOp
from qiskit_nature.second_q.operators import FermionicOp
from qiskit_nature.second_q.mappers import JordanWignerMapper
from quantumrings.toolkit.qiskit import QrEstimatorV1 as Estimator
[2]:
def kronecker_delta_function(n: int, m: int) -> int:
"""An implementation of the Kronecker delta function.
Args:
n (int): The first integer argument.
m (int): The second integer argument.
Returns:
Returns 1 if n = m, else returns 0.
"""
return int(n == m)
[3]:
def create_deuteron_hamiltonian(
N: int, hbar_omega: float = 7.0, V_0: float = -5.68658111
) -> SparsePauliOp:
"""Creates a version of the Deuteron Hamiltonian as a qubit operator.
Args:
N (int): An integer number that represents the dimension of the
basis.
hbar_omega (float, optional): The value of the product of hbar and omega. Defaults to 7.0.
V_0 (float, optional): The value of the potential energy. Defaults to -5.68658111.
Returns:
SparsePauliOp: The qubit-space Hamiltonian that represents the Deuteron.
"""
hamiltonian_terms = {}
for m in range(N):
for n in range(N):
label = "+_{} -_{}".format(str(n), str(m))
coefficient_kinect = (hbar_omega / 2) * (
(2 * n + 3 / 2) * kronecker_delta_function(n, m)
- np.sqrt(n * (n + (1 / 2))) * kronecker_delta_function(n, m + 1)
- np.sqrt((n + 1) * (n + (3 / 2)) * kronecker_delta_function(n, m - 1))
)
hamiltonian_terms[label] = coefficient_kinect
coefficient_potential = (
V_0 * kronecker_delta_function(n, 0) * kronecker_delta_function(n, m)
)
hamiltonian_terms[label] += coefficient_potential
hamiltonian = FermionicOp(hamiltonian_terms, num_spin_orbitals=N)
mapper = JordanWignerMapper()
qubit_hamiltonian = mapper.map(hamiltonian)
if not isinstance(qubit_hamiltonian, SparsePauliOp):
qubit_hamiltonian = qubit_hamiltonian.primitive
return qubit_hamiltonian
[4]:
deuteron_hamiltonians = [create_deuteron_hamiltonian(i) for i in range(1, 5)]
[5]:
for i, hamiltonian in enumerate(deuteron_hamiltonians):
print("Deuteron Hamiltonian: H_{}".format(i + 1))
print(hamiltonian)
print("\n")
Deuteron Hamiltonian: H_1
SparsePauliOp(['I', 'Z'],
coeffs=[-0.21829055+0.j, 0.21829055+0.j])
Deuteron Hamiltonian: H_2
SparsePauliOp(['II', 'IZ', 'XX', 'YY', 'ZI'],
coeffs=[ 5.90670945+0.j, 0.21829055+0.j, -2.14330352+0.j, -2.14330352+0.j,
-6.125 +0.j])
Deuteron Hamiltonian: H_3
SparsePauliOp(['III', 'IIZ', 'IXX', 'IYY', 'IZI', 'XXI', 'YYI', 'ZII'],
coeffs=[15.53170945+0.j, 0.21829055+0.j, -2.14330352+0.j, -2.14330352+0.j,
-6.125 +0.j, -3.91311896+0.j, -3.91311896+0.j, -9.625 +0.j])
Deuteron Hamiltonian: H_4
SparsePauliOp(['IIII', 'IIIZ', 'IIXX', 'IIYY', 'IIZI', 'IXXI', 'IYYI', 'IZII', 'XXII', 'YYII', 'ZIII'],
coeffs=[ 28.65670945+0.j, 0.21829055+0.j, -2.14330352+0.j, -2.14330352+0.j,
-6.125 +0.j, -3.91311896+0.j, -3.91311896+0.j, -9.625 +0.j,
-5.67064811+0.j, -5.67064811+0.j, -13.125 +0.j])
[6]:
theta = Parameter(r"$\theta$")
eta = Parameter(r"$\eta$")
[7]:
wavefunction = QuantumCircuit(1)
wavefunction.ry(theta, 0)
wavefunction.draw("mpl")
[7]:
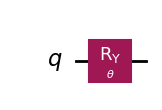
[8]:
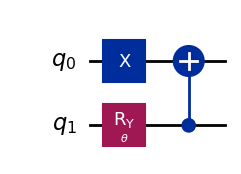
wavefunction2 = QuantumCircuit(2)
wavefunction2.x(0)
wavefunction2.ry(theta, 1)
wavefunction2.cx(1, 0)
wavefunction2.draw("mpl")
[8]:
[9]:
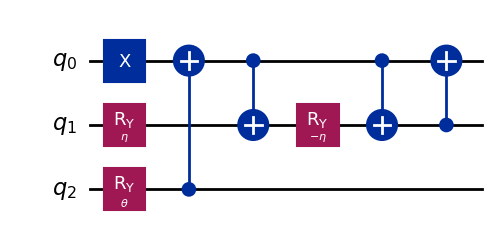
wavefunction3 = QuantumCircuit(3)
wavefunction3.x(0)
wavefunction3.ry(eta, 1)
wavefunction3.ry(theta, 2)
wavefunction3.cx(2, 0)
wavefunction3.cx(0, 1)
wavefunction3.ry(-eta, 1)
wavefunction3.cx(0, 1)
wavefunction3.cx(1, 0)
wavefunction3.draw("mpl")
[9]:
[10]:
ansatz = [wavefunction, wavefunction2, wavefunction3]
[11]:
reference_values = []
print("Exact binding energies calculated through numpy.linalg.eigh \n")
for i, hamiltonian in enumerate(deuteron_hamiltonians):
eigenvalues, eigenstates = np.linalg.eigh(hamiltonian.to_matrix())
reference_values.append(eigenvalues[0])
print("Exact binding energy for H_{}: {}".format(i + 1, eigenvalues[0]))
Exact binding energies calculated through numpy.linalg.eigh
Exact binding energy for H_1: -0.43658110999999966
Exact binding energy for H_2: -1.7491598763215301
Exact binding energy for H_3: -2.0456708984064416
Exact binding energy for H_4: -2.143981030799861
[12]:
print("Results using Estimator for H_1, H_2 and H_3 with the ansatz given in the reference paper \n")
for i in range(3):
seed = 42
algorithm_globals.random_seed = seed
vqe = VQE(Estimator(), ansatz=ansatz[i], optimizer=SLSQP())
vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
binding_energy = vqe_result.optimal_value
print("Binding energy for H_{}: {} MeV".format(i + 1, binding_energy))
Results using Estimator for H_1, H_2 and H_3 with the ansatz given in the reference paper
Binding energy for H_1: -0.43658110960995966 MeV
Binding energy for H_2: -1.7491595316396333 MeV
Binding energy for H_3: -2.04567089825919 MeV
[13]:
def callback(eval_count, parameters, mean, std):
# Overwrites the same line when printing
display("Evaluation: {}, Energy: {}, Std: {}".format(eval_count, mean, std))
clear_output(wait=True)
counts.append(eval_count)
values.append(mean)
params.append(parameters)
deviation.append(std)
[14]:
plots = []
for i in range(3):
counts = []
values = []
params = []
deviation = []
seed = 42
algorithm_globals.random_seed = seed
vqe = VQE(Estimator(), ansatz=ansatz[i], optimizer=COBYLA(), callback=callback)
vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
plots.append([counts, values])
"Evaluation: 45, Energy: -2.0456706360129235, Std: {'shots': 1024}"
[15]:
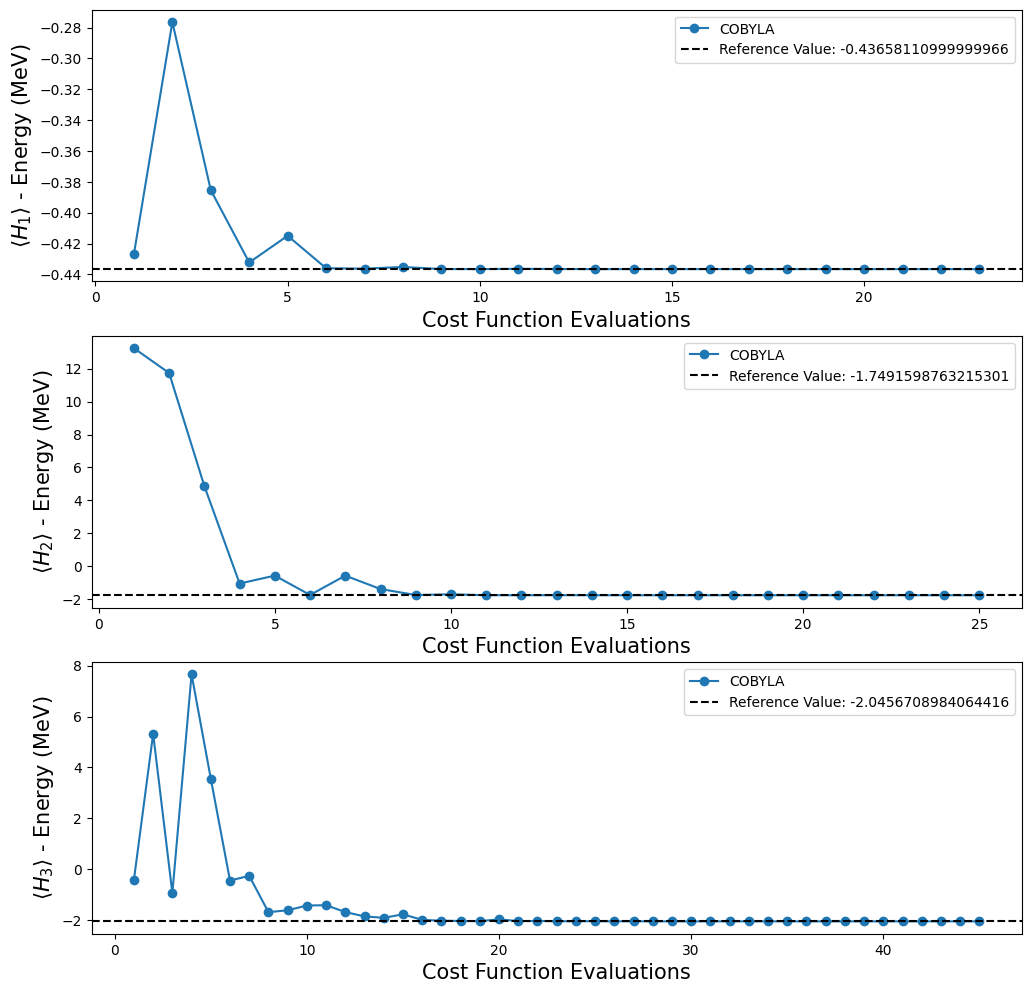
fig, ax = plt.subplots(nrows=3, ncols=1)
fig.set_size_inches((12, 12))
for i, plot in enumerate(plots):
ax[i].plot(plot[0], plot[1], "o-", label="COBYLA")
ax[i].axhline(
y=reference_values[i],
color="k",
linestyle="--",
label=f"Reference Value: {reference_values[i]}",
)
ax[i].legend()
ax[i].set_xlabel("Cost Function Evaluations", fontsize=15)
ax[i].set_ylabel(r"$\langle H_{} \rangle$ - Energy (MeV)".format(i + 1), fontsize=15)
plt.show()
[16]:
twolocal_ansatzes = []
for i in range(1, 5):
ansatz = TwoLocal(
deuteron_hamiltonians[i - 1].num_qubits,
["rz", "ry"],
"cx",
entanglement="full",
reps=i,
initial_state=None,
)
twolocal_ansatzes.append(ansatz)
[17]:
print("Results using Estimator for H_1, H_2, H_3 and H_4 with TwoLocal ansatz \n")
seed = 42
algorithm_globals.random_seed = seed
for i in range(4):
vqe = VQE(Estimator(), ansatz=twolocal_ansatzes[i], optimizer=SLSQP())
vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
binding_energy = vqe_result.optimal_value
print("Binding energy for H_{}:".format(i + 1), binding_energy, "MeV")
Results using Estimator for H_1, H_2, H_3 and H_4 with TwoLocal ansatz
Binding energy for H_1: -0.43658065601161367 MeV
Binding energy for H_2: -1.7491598677360036 MeV
Binding energy for H_3: -2.045670594916378 MeV
Binding energy for H_4: -2.143867103573763 MeV
[18]:
seed = 42
algorithm_globals.random_seed = seed
plots_tl = []
for i in range(4):
counts = []
values = []
params = []
deviation = []
vqe = VQE(
Estimator(),
ansatz=twolocal_ansatzes[i],
optimizer=SLSQP(),
callback=callback,
)
vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
plots_tl.append([counts, values])
"Evaluation: 4148, Energy: -2.143867103581142, Std: {'shots': 1024}"
[19]:
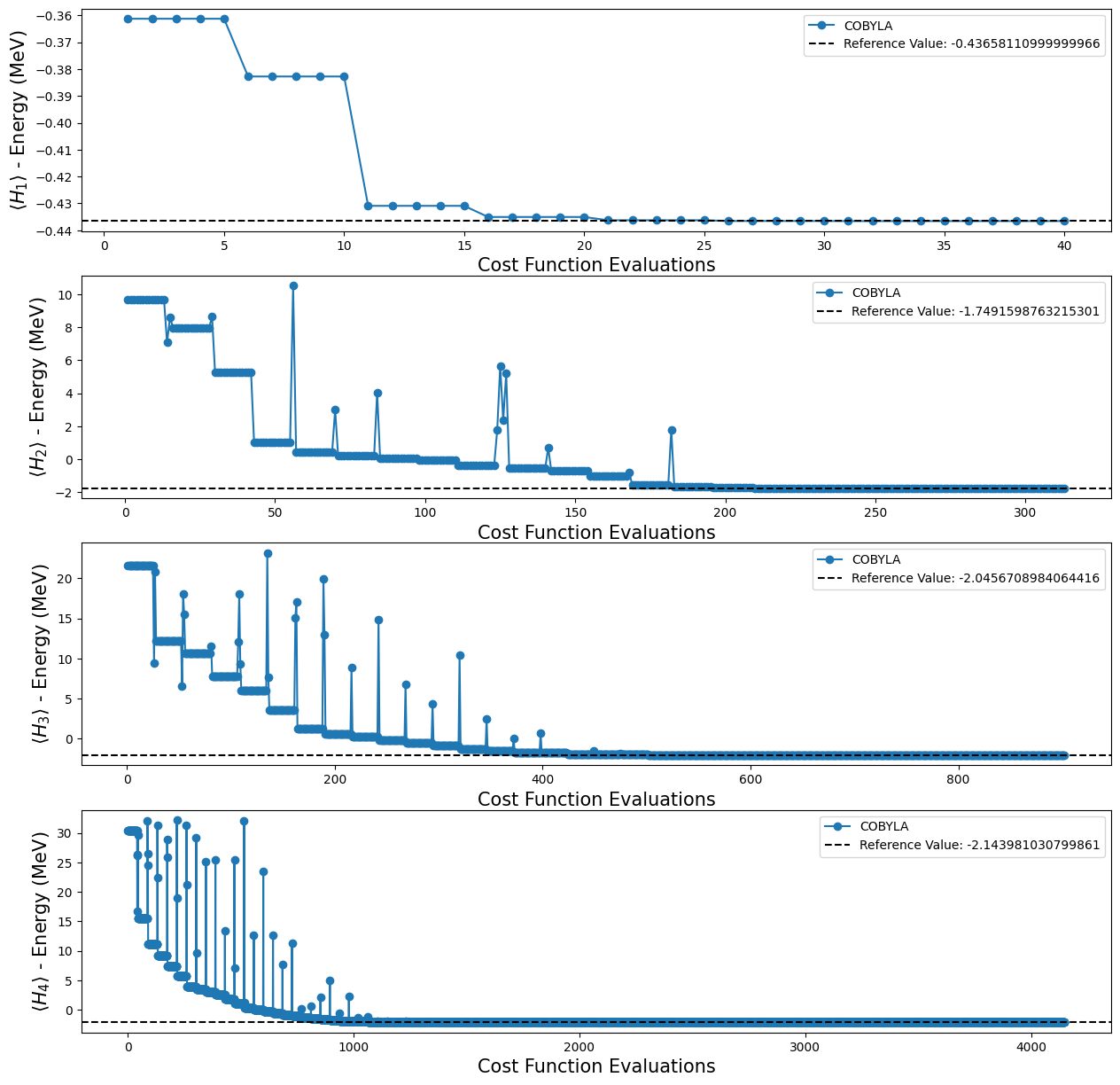
fig, ax = plt.subplots(nrows=4, ncols=1)
fig.set_size_inches((15, 15))
for i, plot in enumerate(plots_tl):
ax[i].plot(plot[0], plot[1], "o-", label="COBYLA")
ax[i].axhline(
y=reference_values[i],
color="k",
linestyle="--",
label=f"Reference Value: {reference_values[i]}",
)
ax[i].legend()
ax[i].set_xlabel("Cost Function Evaluations", fontsize=15)
ax[i].set_ylabel(r"$\langle H_{} \rangle$ - Energy (MeV)".format(i + 1), fontsize=15)
plt.show()
[20]:
def calculate_observables_exp_values(
quantum_circuit: QuantumCircuit, observables: list, angles: list
) -> list:
"""Calculate the expectation value of an observable given the quantum
circuit that represents the wavefunction and a list of parameters.
Args:
quantum_circuit (QuantumCircuit): A parameterized quantum circuit
that represents the wavefunction of the system.
observables (list): A list containing the observables that we want
to know the expectation values.
angles (list): A list with the values that will be used in the
'assign_parameters' method.
Returns:
list_exp_values (list): A list containing the expectation values
of the observables given as input.
"""
list_exp_values = []
for observable in observables:
exp_values = []
for angle in angles:
qc = quantum_circuit.assign_parameters({theta: angle})
result = estimate_observables(
Estimator(),
quantum_state=qc,
observables=[observable],
)
exp_values.append(result[0][0])
list_exp_values.append(exp_values)
return list_exp_values
[21]:
angles = list(np.linspace(-np.pi, np.pi, 100))
observables = [
Pauli("IZ"),
Pauli("ZI"),
Pauli("XX"),
Pauli("YY"),
deuteron_hamiltonians[1],
]
h2_observables_exp_values = calculate_observables_exp_values(wavefunction2, observables, angles)
[22]:
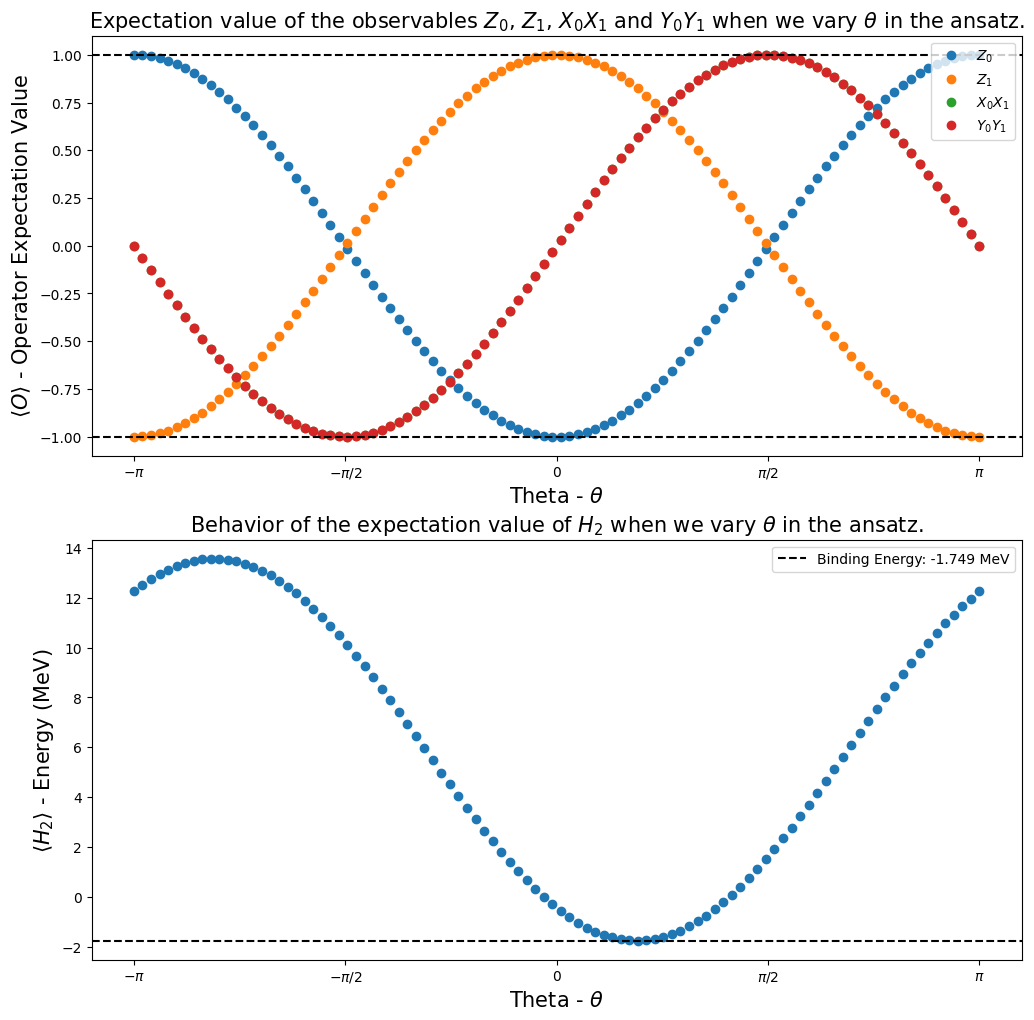
fig, ax = plt.subplots(nrows=2, ncols=1)
fig.set_size_inches((12, 12))
ax[0].plot(angles, h2_observables_exp_values[0], "o", label=r"$Z_0$")
ax[0].plot(angles, h2_observables_exp_values[1], "o", label=r"$Z_1$")
ax[0].plot(angles, h2_observables_exp_values[2], "o", label=r"$X_0X_1$")
ax[0].plot(angles, h2_observables_exp_values[3], "o", label=r"$Y_0Y_1$")
ax[0].axhline(
y=1,
color="k",
linestyle="--",
)
ax[0].axhline(y=-1, color="k", linestyle="--")
ax[0].legend()
ax[0].set_xlabel(r"Theta - $\theta$", fontsize=15)
ax[0].set_ylabel(r"$\langle O \rangle $ - Operator Expectation Value", fontsize=15)
ax[0].set_xticks(
[-np.pi, -np.pi / 2, 0, np.pi / 2, np.pi],
labels=[r"$-\pi$", r"$-\pi/2$", "0", r"$\pi/2$", r"$\pi$"],
)
ax[0].set_title(
r"Expectation value of the observables $Z_0$, $Z_1$, $X_0X_1$ and $Y_0Y_1$ when we vary $\theta$ in the ansatz.",
fontsize=15,
)
ax[1].plot(angles, h2_observables_exp_values[4], "o")
ax[1].axhline(
y=reference_values[1],
color="k",
linestyle="--",
label="Binding Energy: {} MeV".format(np.round(reference_values[1], 3)),
)
ax[1].legend()
ax[1].set_xlabel(r"Theta - $\theta$", fontsize=15)
ax[1].set_ylabel(r"$\langle H_2 \rangle $ - Energy (MeV)", fontsize=15)
ax[1].set_xticks(
[-np.pi, -np.pi / 2, 0, np.pi / 2, np.pi],
labels=[r"$-\pi$", r"$-\pi/2$", "0", r"$\pi/2$", r"$\pi$"],
)
ax[1].set_title(
r"Behavior of the expectation value of $H_2$ when we vary $\theta$ in the ansatz.", fontsize=15
)
plt.show()
[ ]: