07-Finance Tutorial-Pricing Asian Barrier Spreads
[ ]:
#this example is at:
# https://qiskit-community.github.io/qiskit-finance/tutorials/07_asian_barrier_spread_pricing.html
[1]:
import matplotlib.pyplot as plt
from scipy.interpolate import griddata
%matplotlib inline
import numpy as np
from qiskit import QuantumRegister, QuantumCircuit, AncillaRegister, transpile
from qiskit.circuit.library import IntegerComparator, WeightedAdder, LinearAmplitudeFunction
from qiskit_algorithms import IterativeAmplitudeEstimation, EstimationProblem
#from qiskit_aer.primitives import Sampler
from qiskit_finance.circuit.library import LogNormalDistribution
from quantumrings.toolkit.qiskit import QrSamplerV1 as Sampler
[2]:
# number of qubits per dimension to represent the uncertainty
num_uncertainty_qubits = 2
# parameters for considered random distribution
S = 2.0 # initial spot price
vol = 0.4 # volatility of 40%
r = 0.05 # annual interest rate of 4%
T = 40 / 365 # 40 days to maturity
# resulting parameters for log-normal distribution
mu = (r - 0.5 * vol**2) * T + np.log(S)
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2 / 2)
variance = (np.exp(sigma**2) - 1) * np.exp(2 * mu + sigma**2)
stddev = np.sqrt(variance)
# lowest and highest value considered for the spot price; in between, an equidistant discretization is considered.
low = np.maximum(0, mean - 3 * stddev)
high = mean + 3 * stddev
# map to higher dimensional distribution
# for simplicity assuming dimensions are independent and identically distributed)
dimension = 2
num_qubits = [num_uncertainty_qubits] * dimension
low = low * np.ones(dimension)
high = high * np.ones(dimension)
mu = mu * np.ones(dimension)
cov = sigma**2 * np.eye(dimension)
# construct circuit
u = LogNormalDistribution(num_qubits=num_qubits, mu=mu, sigma=cov, bounds=(list(zip(low, high))))
[3]:
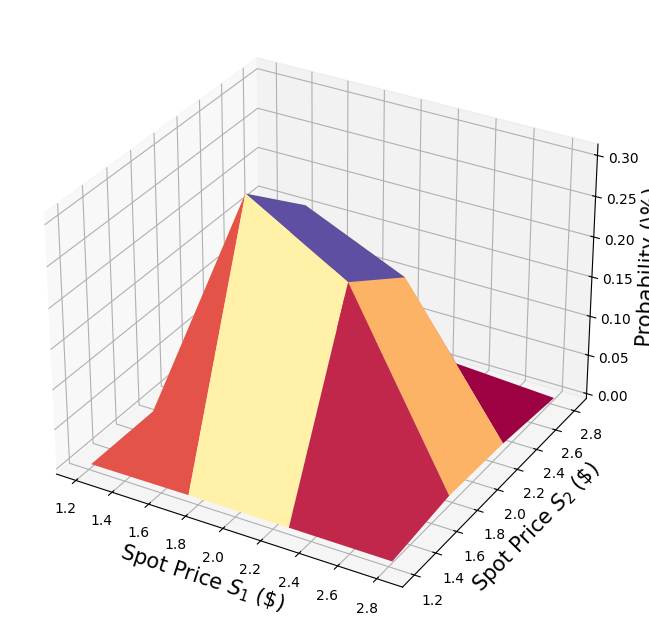
# plot PDF of uncertainty model
x = [v[0] for v in u.values]
y = [v[1] for v in u.values]
z = u.probabilities
# z = map(float, z)
# z = list(map(float, z))
resolution = np.array([2**n for n in num_qubits]) * 1j
grid_x, grid_y = np.mgrid[min(x) : max(x) : resolution[0], min(y) : max(y) : resolution[1]]
grid_z = griddata((x, y), z, (grid_x, grid_y))
plt.figure(figsize=(10, 8))
ax = plt.axes(projection="3d")
ax.plot_surface(grid_x, grid_y, grid_z, cmap=plt.cm.Spectral)
ax.set_xlabel("Spot Price $S_1$ (\$)", size=15)
ax.set_ylabel("Spot Price $S_2$ (\$)", size=15)
ax.set_zlabel("Probability (\%)", size=15)
plt.show()
[4]:
# determine number of qubits required to represent total loss
weights = []
for n in num_qubits:
for i in range(n):
weights += [2**i]
# create aggregation circuit
agg = WeightedAdder(sum(num_qubits), weights)
n_s = agg.num_sum_qubits
n_aux = agg.num_qubits - n_s - agg.num_state_qubits # number of additional qubits
[5]:
# set the strike price (should be within the low and the high value of the uncertainty)
strike_price_1 = 3
strike_price_2 = 4
# set the barrier threshold
barrier = 2.5
# map strike prices and barrier threshold from [low, high] to {0, ..., 2^n-1}
max_value = 2**n_s - 1
low_ = low[0]
high_ = high[0]
mapped_strike_price_1 = (
(strike_price_1 - dimension * low_) / (high_ - low_) * (2**num_uncertainty_qubits - 1)
)
mapped_strike_price_2 = (
(strike_price_2 - dimension * low_) / (high_ - low_) * (2**num_uncertainty_qubits - 1)
)
mapped_barrier = (barrier - low) / (high - low) * (2**num_uncertainty_qubits - 1)
[6]:
# condition and condition result
conditions = []
barrier_thresholds = [2] * dimension
n_aux_conditions = 0
for i in range(dimension):
# target dimension of random distribution and corresponding condition (which is required to be True)
comparator = IntegerComparator(num_qubits[i], mapped_barrier[i] + 1, geq=False)
n_aux_conditions = max(n_aux_conditions, comparator.num_ancillas)
conditions += [comparator]
[7]:
# set the approximation scaling for the payoff function
c_approx = 0.25
# setup piecewise linear objective fcuntion
breakpoints = [0, mapped_strike_price_1, mapped_strike_price_2]
slopes = [0, 1, 0]
offsets = [0, 0, mapped_strike_price_2 - mapped_strike_price_1]
f_min = 0
f_max = mapped_strike_price_2 - mapped_strike_price_1
objective = LinearAmplitudeFunction(
n_s,
slopes,
offsets,
domain=(0, max_value),
image=(f_min, f_max),
rescaling_factor=c_approx,
breakpoints=breakpoints,
)
[8]:
# number of qubits per dimension to represent the uncertainty
num_uncertainty_qubits = 2
# parameters for considered random distribution
S = 2.0 # initial spot price
vol = 0.4 # volatility of 40%
r = 0.05 # annual interest rate of 4%
T = 40 / 365 # 40 days to maturity
# resulting parameters for log-normal distribution
mu = (r - 0.5 * vol**2) * T + np.log(S)
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2 / 2)
variance = (np.exp(sigma**2) - 1) * np.exp(2 * mu + sigma**2)
stddev = np.sqrt(variance)
# lowest and highest value considered for the spot price; in between, an equidistant discretization is considered.
low = np.maximum(0, mean - 3 * stddev)
high = mean + 3 * stddev
# map to higher dimensional distribution
# for simplicity assuming dimensions are independent and identically distributed)
dimension = 2
num_qubits = [num_uncertainty_qubits] * dimension
low = low * np.ones(dimension)
high = high * np.ones(dimension)
mu = mu * np.ones(dimension)
cov = sigma**2 * np.eye(dimension)
# construct circuit
u = LogNormalDistribution(num_qubits=num_qubits, mu=mu, sigma=cov, bounds=list(zip(low, high)))
[9]:
# define overall multivariate problem
qr_state = QuantumRegister(u.num_qubits, "state") # to load the probability distribution
qr_obj = QuantumRegister(1, "obj") # to encode the function values
ar_sum = AncillaRegister(n_s, "sum") # number of qubits used to encode the sum
ar_cond = AncillaRegister(len(conditions) + 1, "conditions")
ar = AncillaRegister(
max(n_aux, n_aux_conditions, objective.num_ancillas), "work"
) # additional qubits
objective_index = u.num_qubits
# define the circuit
asian_barrier_spread = QuantumCircuit(qr_state, qr_obj, ar_cond, ar_sum, ar)
# load the probability distribution
asian_barrier_spread.append(u, qr_state)
# apply the conditions
for i, cond in enumerate(conditions):
state_qubits = qr_state[(num_uncertainty_qubits * i) : (num_uncertainty_qubits * (i + 1))]
asian_barrier_spread.append(cond, state_qubits + [ar_cond[i]] + ar[: cond.num_ancillas])
# aggregate the conditions on a single qubit
asian_barrier_spread.mcx(ar_cond[:-1], ar_cond[-1])
# apply the aggregation function controlled on the condition
asian_barrier_spread.append(agg.control(), [ar_cond[-1]] + qr_state[:] + ar_sum[:] + ar[:n_aux])
# apply the payoff function
asian_barrier_spread.append(objective, ar_sum[:] + qr_obj[:] + ar[: objective.num_ancillas])
# uncompute the aggregation
asian_barrier_spread.append(
agg.inverse().control(), [ar_cond[-1]] + qr_state[:] + ar_sum[:] + ar[:n_aux]
)
# uncompute the conditions
asian_barrier_spread.mcx(ar_cond[:-1], ar_cond[-1])
for j, cond in enumerate(reversed(conditions)):
i = len(conditions) - j - 1
state_qubits = qr_state[(num_uncertainty_qubits * i) : (num_uncertainty_qubits * (i + 1))]
asian_barrier_spread.append(
cond.inverse(), state_qubits + [ar_cond[i]] + ar[: cond.num_ancillas]
)
print(asian_barrier_spread.draw())
print("objective qubit index", objective_index)
┌───────┐┌──────┐ ┌───────────┐ ┌──────────────┐»
state_0: ┤0 ├┤0 ├─────────────┤1 ├──────┤1 ├»
│ ││ │ │ │ │ │»
state_1: ┤1 ├┤1 ├─────────────┤2 ├──────┤2 ├»
│ P(X) ││ │┌──────┐ │ │ │ │»
state_2: ┤2 ├┤ ├┤0 ├─────┤3 ├──────┤3 ├»
│ ││ ││ │ │ │ │ │»
state_3: ┤3 ├┤ ├┤1 ├─────┤4 ├──────┤4 ├»
└───────┘│ ││ │ │ │┌────┐│ │»
obj: ─────────┤ ├┤ ├─────┤ ├┤3 ├┤ ├»
│ ││ │ │ ││ ││ │»
conditions_0: ─────────┤2 ├┤ ├──■──┤ ├┤ ├┤ ├»
│ cmp ││ │ │ │ ││ ││ │»
conditions_1: ─────────┤ ├┤2 ├──■──┤ ├┤ ├┤ ├»
│ ││ cmp │┌─┴─┐│ c_adder ││ ││ c_adder_dg │»
conditions_2: ─────────┤ ├┤ ├┤ X ├┤0 ├┤ ├┤0 ├»
│ ││ │└───┘│ ││ ││ │»
sum_0: ─────────┤ ├┤ ├─────┤5 ├┤0 ├┤5 ├»
│ ││ │ │ ││ F ││ │»
sum_1: ─────────┤ ├┤ ├─────┤6 ├┤1 ├┤6 ├»
│ ││ │ │ ││ ││ │»
sum_2: ─────────┤ ├┤ ├─────┤7 ├┤2 ├┤7 ├»
│ ││ │ │ ││ ││ │»
work_0: ─────────┤3 ├┤3 ├─────┤8 ├┤4 ├┤8 ├»
└──────┘└──────┘ │ ││ ││ │»
work_1: ──────────────────────────────┤9 ├┤5 ├┤9 ├»
│ ││ ││ │»
work_2: ──────────────────────────────┤10 ├┤6 ├┤10 ├»
└───────────┘└────┘└──────────────┘»
« ┌─────────┐
« state_0: ────────────────┤0 ├
« │ │
« state_1: ────────────────┤1 ├
« ┌─────────┐│ │
« state_2: ─────┤0 ├┤ ├
« │ ││ │
« state_3: ─────┤1 ├┤ ├
« │ ││ │
« obj: ─────┤ ├┤ ├
« │ ││ │
«conditions_0: ──■──┤ ├┤2 ├
« │ │ ││ cmp_dg │
«conditions_1: ──■──┤2 ├┤ ├
« ┌─┴─┐│ cmp_dg ││ │
«conditions_2: ┤ X ├┤ ├┤ ├
« └───┘│ ││ │
« sum_0: ─────┤ ├┤ ├
« │ ││ │
« sum_1: ─────┤ ├┤ ├
« │ ││ │
« sum_2: ─────┤ ├┤ ├
« │ ││ │
« work_0: ─────┤3 ├┤3 ├
« └─────────┘└─────────┘
« work_1: ───────────────────────────
«
« work_2: ───────────────────────────
«
objective qubit index 4
[10]:
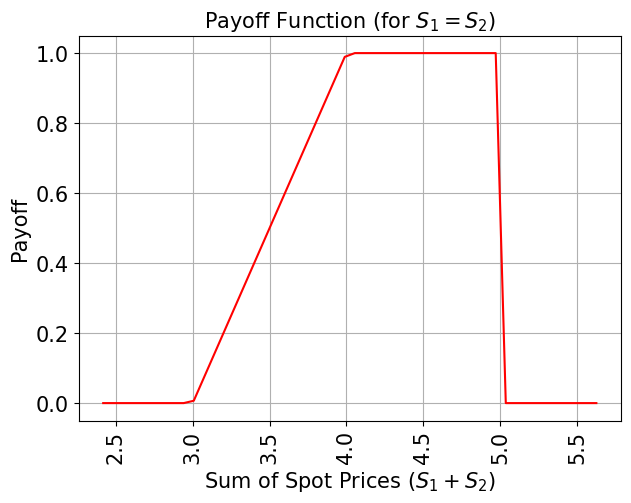
# plot exact payoff function
plt.figure(figsize=(7, 5))
x = np.linspace(sum(low), sum(high))
y = (x <= 5) * np.minimum(np.maximum(0, x - strike_price_1), strike_price_2 - strike_price_1)
plt.plot(x, y, "r-")
plt.grid()
plt.title("Payoff Function (for $S_1 = S_2$)", size=15)
plt.xlabel("Sum of Spot Prices ($S_1 + S_2)$", size=15)
plt.ylabel("Payoff", size=15)
plt.xticks(size=15, rotation=90)
plt.yticks(size=15)
plt.show()
[11]:
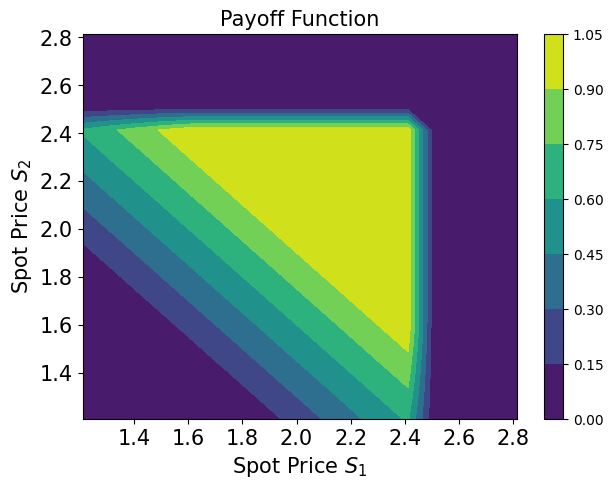
# plot contour of payoff function with respect to both time steps, including barrier
plt.figure(figsize=(7, 5))
z = np.zeros((17, 17))
x = np.linspace(low[0], high[0], 17)
y = np.linspace(low[1], high[1], 17)
for i, x_ in enumerate(x):
for j, y_ in enumerate(y):
z[i, j] = np.minimum(
np.maximum(0, x_ + y_ - strike_price_1), strike_price_2 - strike_price_1
)
if x_ > barrier or y_ > barrier:
z[i, j] = 0
plt.title("Payoff Function", size=15)
plt.contourf(x, y, z)
plt.colorbar()
plt.xlabel("Spot Price $S_1$", size=15)
plt.ylabel("Spot Price $S_2$", size=15)
plt.xticks(size=15)
plt.yticks(size=15)
plt.show()
[12]:
# evaluate exact expected value
sum_values = np.sum(u.values, axis=1)
payoff = np.minimum(np.maximum(sum_values - strike_price_1, 0), strike_price_2 - strike_price_1)
leq_barrier = [np.max(v) <= barrier for v in u.values]
exact_value = np.dot(u.probabilities[leq_barrier], payoff[leq_barrier])
print("exact expected value:\t%.4f" % exact_value)
exact expected value: 0.8023
[13]:
num_state_qubits = asian_barrier_spread.num_qubits - asian_barrier_spread.num_ancillas
print("state qubits: ", num_state_qubits)
transpiled = transpile(asian_barrier_spread, basis_gates=["u", "cx"])
print("circuit width:", transpiled.width())
print("circuit depth:", transpiled.depth())
state qubits: 5
circuit width: 14
circuit depth: 6049
[14]:
asian_barrier_spread_measure = asian_barrier_spread.measure_all(inplace=False)
sampler = Sampler()
job = sampler.run(asian_barrier_spread_measure)
[15]:
# evaluate the result
value = 0
probabilities = job.result().quasi_dists[0].binary_probabilities()
for i, prob in probabilities.items():
if prob > 1e-4 and i[-num_state_qubits:][0] == "1":
value += prob
# map value to original range
mapped_value = objective.post_processing(value) / (2**num_uncertainty_qubits - 1) * (high_ - low_)
print("Exact Operator Value: %.4f" % value)
print("Mapped Operator value: %.4f" % mapped_value)
print("Exact Expected Payoff: %.4f" % exact_value)
Exact Operator Value: 0.6318
Mapped Operator value: 0.8357
Exact Expected Payoff: 0.8023
[16]:
# set target precision and confidence level
epsilon = 0.01
alpha = 0.05
problem = EstimationProblem(
state_preparation=asian_barrier_spread,
objective_qubits=[objective_index],
post_processing=objective.post_processing,
)
# construct amplitude estimation
ae = IterativeAmplitudeEstimation(
epsilon, alpha=alpha, sampler=Sampler(options={"shots": 100, "seed": 75})
)
[17]:
result = ae.estimate(problem)
[18]:
conf_int = (
np.array(result.confidence_interval_processed)
/ (2**num_uncertainty_qubits - 1)
* (high_ - low_)
)
print("Exact value: \t%.4f" % exact_value)
print(
"Estimated value:\t%.4f"
% (result.estimation_processed / (2**num_uncertainty_qubits - 1) * (high_ - low_))
)
print("Confidence interval: \t[%.4f, %.4f]" % tuple(conf_int))
Exact value: 0.8023
Estimated value: 0.8283
Confidence interval: [0.8202, 0.8363]
[ ]: