08-Finance Tutorial-Pricing Fixed-Income Assets

#where to find this code?
#https://qiskit-community.github.io/qiskit-finance/tutorials/08_fixed_income_pricing.html

import matplotlib.pyplot as plt

%matplotlib inline
import numpy as np
from qiskit import QuantumCircuit
from qiskit_algorithms import IterativeAmplitudeEstimation, EstimationProblem
#from qiskit_aer.primitives import Sampler
from qiskit_finance.circuit.library import NormalDistribution

from quantumrings.toolkit.qiskit import QrSamplerV1 as Sampler

# can be used in case a principal component analysis has been done to derive the uncertainty model, ignored in this example.
A = np.eye(2)
b = np.zeros(2)

# specify the number of qubits that are used to represent the different dimenions of the uncertainty model
num_qubits = [2, 2]

# specify the lower and upper bounds for the different dimension
low = [0, 0]
high = [0.12, 0.24]
mu = [0.12, 0.24]
sigma = 0.01 * np.eye(2)

# construct corresponding distribution
bounds = list(zip(low, high))
u = NormalDistribution(num_qubits, mu, sigma, bounds)

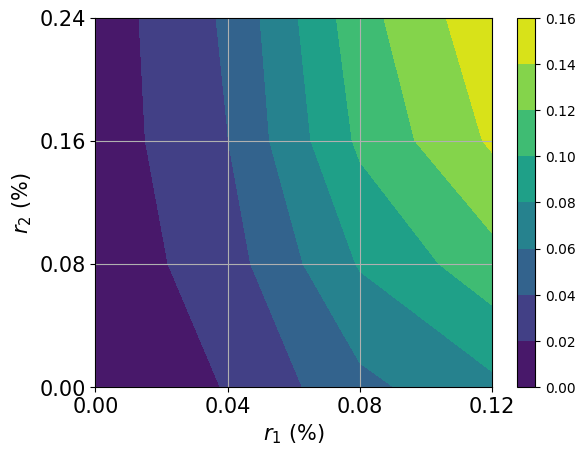
# plot contour of probability density function
x = np.linspace(low[0], high[0], 2 ** num_qubits[0])
y = np.linspace(low[1], high[1], 2 ** num_qubits[1])
z = u.probabilities.reshape(2 ** num_qubits[0], 2 ** num_qubits[1])
plt.contourf(x, y, z)
plt.xticks(x, size=15)
plt.yticks(y, size=15)
plt.grid()
plt.xlabel("$r_1$ (%)", size=15)
plt.ylabel("$r_2$ (%)", size=15)
plt.colorbar()
plt.show()

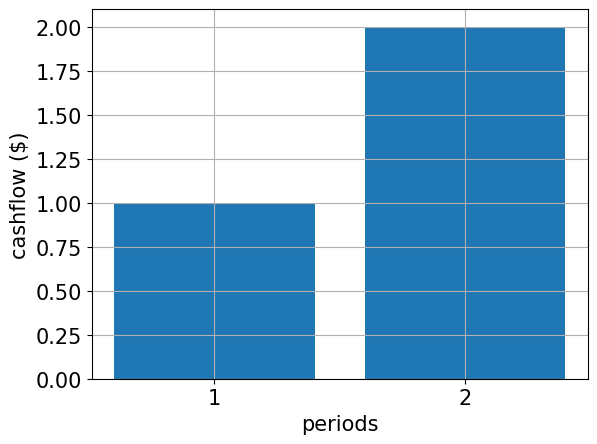
# specify cash flow
cf = [1.0, 2.0]
periods = range(1, len(cf) + 1)

# plot cash flow
plt.bar(periods, cf)
plt.xticks(periods, size=15)
plt.yticks(size=15)
plt.grid()
plt.xlabel("periods", size=15)
plt.ylabel("cashflow ($)", size=15)
plt.show()

# estimate real value
cnt = 0
exact_value = 0.0
for x1 in np.linspace(low[0], high[0], pow(2, num_qubits[0])):
    for x2 in np.linspace(low[1], high[1], pow(2, num_qubits[1])):
        prob = u.probabilities[cnt]
        for t in range(len(cf)):
            # evaluate linear approximation of real value w.r.t. interest rates
            exact_value += prob * (
                cf[t] / pow(1 + b[t], t + 1)
                - (t + 1) * cf[t] * np.dot(A[:, t], np.asarray([x1, x2])) / pow(1 + b[t], t + 2)
            )
        cnt += 1
print("Exact value:    \t%.4f" % exact_value)

Exact value:            2.1942

# specify approximation factor
c_approx = 0.125

# create fixed income pricing application
from qiskit_finance.applications.estimation import FixedIncomePricing

fixed_income = FixedIncomePricing(
    num_qubits=num_qubits,
    pca_matrix=A,
    initial_interests=b,
    cash_flow=cf,
    rescaling_factor=c_approx,
    bounds=bounds,
    uncertainty_model=u,
)

fixed_income._objective.draw()

     ┌────┐
q_0: ┤0   ├
     │    │
q_1: ┤1   ├
     │    │
q_2: ┤2 F ├
     │    │
q_3: ┤3   ├
     │    │
q_4: ┤4   ├
     └────┘

fixed_income_circ = QuantumCircuit(fixed_income._objective.num_qubits)

# load probability distribution
fixed_income_circ.append(u, range(u.num_qubits))

# apply function
fixed_income_circ.append(fixed_income._objective, range(fixed_income._objective.num_qubits))

fixed_income_circ.draw()

     ┌───────┐┌────┐
q_0: ┤0      ├┤0   ├
     │       ││    │
q_1: ┤1      ├┤1   ├
     │  P(X) ││    │
q_2: ┤2      ├┤2 F ├
     │       ││    │
q_3: ┤3      ├┤3   ├
     └───────┘│    │
q_4: ─────────┤4   ├
              └────┘

# set target precision and confidence level
epsilon = 0.01
alpha = 0.05

# construct amplitude estimation
problem = fixed_income.to_estimation_problem()

ae = IterativeAmplitudeEstimation(
    epsilon_target=epsilon, alpha=alpha, sampler=Sampler(run_options={"shots": 100, "seed": 75})
)

result = ae.estimate(problem)

conf_int = np.array(result.confidence_interval_processed)
print("Exact value:        \t%.4f" % exact_value)
print("Estimated value:    \t%.4f" % (fixed_income.interpret(result)))
print("Confidence interval:\t[%.4f, %.4f]" % tuple(conf_int))

Exact value:            2.1942
Estimated value:        2.3274
Confidence interval:    [2.2787, 2.3761]