Simon’s Algorithm

In 1994, Daniel Simon found an oracle-based function with an exponential speedup. The Quantum Fourier Transform and Shor’s algorithm were invented around the same time. Simon’s algorithm uses quantum parallelism and quantum interference and it is a very good teaching example.

Problem Definition

Assume we have an oracle function that maps n-bits to n-bits. i.e., \(f∶\left\{0,1\right\}^n \mapsto \left\{0,1\right\}^n\). Also, assume that the oracle function is guaranteed to satisfy the condition: \(f(x)= f(y) \Longleftrightarrow y=x \oplus a\). Simon’s problem is then querying the oracle function and determining whether the hidden string \(a= 0^n\) or \(a\neq 0^n\). If \(a= 0^n\), then the oracle function is a one-to-one function. If \(a\neq 0^n\), then the function is a two-to-one function.

A one-to-one function produces a unique output for each input. A two-to-one function produces a unique output for two inputs. This is illustrated in the following examples.

EXAMPLE: ONE-TO-ONE FUNCTION:

\(x\)

000

001

010

011

100

101

110

111

\(f(x)\)

111

110

101

100

011

010

001

000

Table 1

EXAMPLE: TWO-TO-ONE FUNCTION:

\(x\)

000

001

010

011

100

101

110

111

\(f(x)\)

011

010

010

011

000

001

001

000

Table 2

Table 1 illustrates a two-to-one function. By examining this table, we can trace four distinct values: \(000, 001, 010, 011\). Each distinct value is repeated twice. Let us choose one of these distinct values: \(011\). The corresponding \(x\) values are \(000\) and \(011\). The hidden string \(a= 000 \oplus 011 = 011\). We can verify this for other distinct values.

From the table, we can recognize the following property:

\[f(x)=f(x \bigoplus a)\]

We know that \(x \oplus a \oplus a= x\), we can rewrite the above equation.

\[f(x) = f(x \bigoplus a) = f(x \oplus a \oplus a)\]

This equation means \(f(x)\) is periodic with the period a, in bitwise \(mod 2\) operation. Solving Simon’s problem classically is somewhat challenging. One way to determine the hidden string a, is to keep calling the oracle function until we find two repeat values. Let us assume that we had to call the oracle function i times to detect a repeat value. The number of pairs we may have compared is \(\frac{i(i-1)}{2} \approx\ 2^n\). This is the minimum number of pairs that need to be examined before determining a. The complexity of this classical method is \(O(2^\frac{n}{2})\), exponential to n. Therefore, the number of times we call the oracle function grows exponentially with n, the number of bits in the hidden string a. The following figure shows the block diagram used to solve Simon’s problem.

Simon's Algorithm Block Diagram.

See [13] for a detailed explanation of the block diagram and the step-by-step math. The following figure [19] shows the quantum circuit that implements Simon’s algorithm for the hidden string \(011b = 3\)

Simon's Algorithm Quantum Circuit.

Note

Be sure to use your API token and your account name.

Step 1. Import the required modules and obtain the backend

import QuantumRingsLib
from QuantumRingsLib import QuantumRegister, AncillaRegister, ClassicalRegister, QuantumCircuit
from QuantumRingsLib import QuantumRingsProvider
from QuantumRingsLib import job_monitor
from QuantumRingsLib import JobStatus
from matplotlib import pyplot as plt
import numpy as np

provider = QuantumRingsProvider(token =<YOUR_TOKEN_HERE>, name=<YOUR_ACCOUNT_NAME_HERE>)
backend = provider.get_backend("scarlet_quantum_rings")
shots = 100

provider.active_account()

Step 2. Define the core methods

def plot_histogram (counts, title=""):
    """
    Plots the histogram of the counts

    Args:

        counts (dict):
            The dictionary containing the counts of states

        titles (str):
            A title for the graph.

    Returns:
        None

    """
    fig, ax = plt.subplots(figsize =(10, 7))
    plt.xlabel("States")
    plt.ylabel("Counts")
    mylist = [key for key, val in counts.items() for _ in range(val)]

    unique, inverse = np.unique(mylist, return_inverse=True)
    bin_counts = np.bincount(inverse)

    plt.bar(unique, bin_counts)

    maxFreq = max(counts.values())
    plt.ylim(ymax=np.ceil(maxFreq / 10) * 10 if maxFreq % 10 else maxFreq + 10)
    # Show plot
    plt.title(title)
    plt.show()
    return

def simons_func (qc, a):
    n = qc.num_qubits // 2

    # put the first half - REG 1 through H gate
    for i in range (n):
        qc.h(i)

    qc.barrier()

    # build the oracle function
    for i in range (n):
        if ( 0!= (( 1 << i) & a)):
            for j in range (n):
                qc.cx(q[i], q[j+n])
    qc.barrier()

    # measure the lower half REG 2
    for i in range (n, qc.num_qubits):
        qc.measure(i,i)
    qc.barrier()

    # Apply H transform to REG 1
    for i in range (n):
        qc.h(i)
    qc.barrier()

    # Finally measure the first half  REG 1
    for i in range (n):
        qc.measure(i,i)

    return

Step 3. Execute the algorithm and plot the results

# obtain the hidden string from the user
hiddenstring = int(input("Enter the hidden string as a binary value: "), 2)

#determine the number of qubits required to represent the hidden string
numberofqubits = hiddenstring.bit_length()

# add a qubit for the ancilla register
numberofqubits *= 2

q = QuantumRegister(numberofqubits , 'q')
c = ClassicalRegister(numberofqubits , 'c')
qc = QuantumCircuit(q, c)

simons_func(qc, hiddenstring )

job = backend.run(qc, shots=shots)
job_monitor(job)
result = job.result()
counts = result.get_counts()

# plot the histogram for REG 1 alone
res_plot = {}
for i in counts.keys():
    inp = i[numberofqubits // 2:]
    if inp in res_plot:
        res_plot[inp] += counts[i]
    else:
        res_plot[inp] = counts[i]
plot_histogram(res_plot, "")

An example histogram is shown below for the hidden string \(10011001\).

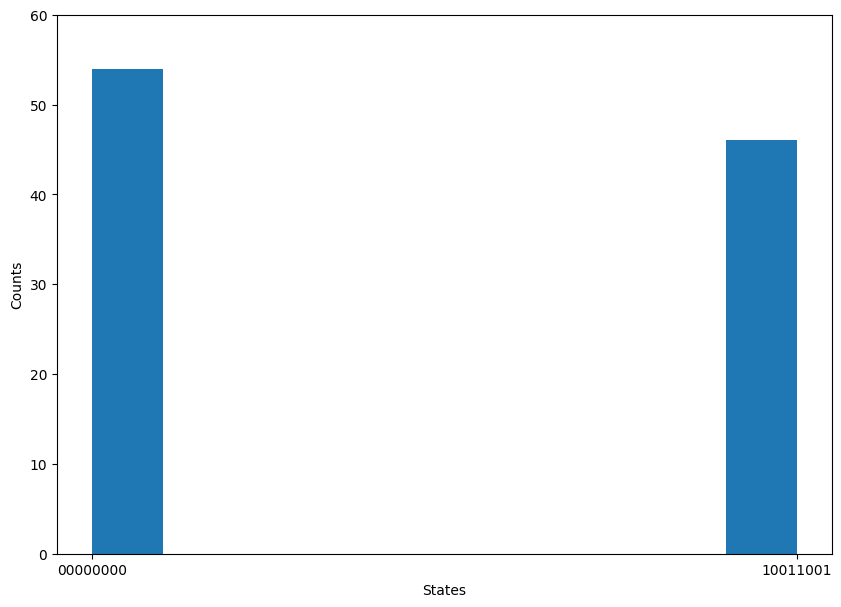
A plot of the GHZ state.

We run this function n times and get n strings: \(y_1y_2y_3\ldots y_n\). With these n strings, we have n equations: \(a\cdot y_1=0; a\cdot y_2=0; \ldots a\cdot y_n=0\). If \(y_1y_2y_3\ldots y_n\) are linearly independent, then we can quickly solve this system of equations, and the total number of possible substrings is \(2^n\). Say, if we tried this algorithm for a few times more than n, then the probability of getting n linearly independent strings is:

\[P_r=\left(1-\frac{1}{2^1}\right) \left(1-\frac{1}{2^2}\right) \ldots \left(1-\frac{1}{2^n}\right) > \frac{1}{4}\]

If we are not finding the set of linearly independent string :math: y_i, we can keep calling the function beyond the n attempts, until we can determine a. If we totally cannot get the required set of linearly independent strings, then it means \(a= 0^n\). The probability of this occurrence is given by:

\[P_r=\left(1-\frac{1}{4}\right)^{4x} < e^{-x}\]

If we try this for \(x=10\) times, the error rate is approximately \(1\) in \(10000\). The advantage of this algorithm is that the number of times we need to try beyond n is not dependent on n. The classical algorithm requires \(2^\frac{n}{2}\) steps, whereas the quantum version requires a little over n steps, which is an exponential advantage.