Solving the Max-Cut problem using QAOA¶
Note
Source code is at the end of this page.
Introduction
Given a graph \(G=\left[V,E\right]\), with \(V\) vertices and \(E\) edges, a cut \(S\) slices the graph into two disjoint subgraphs \(G_1=\left(V_1,E_1\right)\) and \(G_2=\left(V_2,E_2\right)\) with \(V_1\ \cap\ V_2=0\). The size of the cut is the number of edges connecting the two subsets.
The maximum cut is an operation that partitions the graph’s vertices \(V\) into two complementary sets \(V_1\) and \(V_2\), such that the number of edges between the sets \(V_1\) and \(V_2\) is as large as possible.
The goal of the Max-Cut problem is to find the algorithm that maximizes the cut. Max-Cut is an NP-Hard problem. Hence there are no known polynomial-time algorithms. The best-known classical algorithm is a polynomial-time approximation algorithm by Goemans and Williamson using semidefinite programming and randomized rounding with an approximation ratio of 0.878 [7].
For any cut \(S\ \subseteq V\), and a given vertex \(i\ \in V\), if \(i\ \in S\), let us define \(z_i=1\), and if \(i\ \notin S\), let us define \(z_i=-1\). Then an edge \(j,k\) is cut only if \(\frac{1}{2}\left(1-z_jz_k\right)=1\) (that is, belongs to one set A) and 0 (that is, belongs to the other set B) if not cut. With these definitions, we can write a quadratic program [1] for this problem as follows:
The following graph illustrates the Max-Cut process.
In the above figure (a), the circular loop with dotted lines illustrates the Max-Cut operation. The vertices of the partitioned sub-graphs are colored in blue and red. In the figure (b), the dark shaded edges form the maximum cut set.
Consider a graph of \(n\) vertices and an edge set \(\left\langle j,k\right\rangle\) of size \(m\). Our goal is to find the algorithm that performs a maximum cut of this graph along the edge set \(\left\langle j,k\right\rangle\). The objective function of this problem counts the number of edges crossing the partition:
Assume that we have a quantum computer of \(n\) qubits, with each of the qubits representing the \(n\)-vertices of a graph. The \(2^n\) superposition states of the \(n\) qubits can encode the possible partitions of the graph. Recall that the eigenvalues of the Pauli operator \(\sigma_z\) are \(-1\) and \(+1\). Therefore, in the computational basis, the qubits can encode the information on which side of the cut they belong in terms of the Pauli operator \(\sigma_z\). With this understanding, we can write the quantum analog of equation ( 1 ) as follows:
Plugging equation (3) into the QAOA equation (17) in the previous section,
For the case when \(p=1\), the above equation becomes:
In equation ( 5 ), the terms corresponding to the phase separation and mixing operators that do not involve qubits \(j\) and \(k\) do not commute through \(C_{\left\langle j,k\right\rangle}\) and gets cancelled.
With some math work we can see that the operator \(U^\dagger\left(C,\gamma_1\right)..U^\dagger\left(B,\beta_p\right)C_{\left\langle j,k\right\rangle}U(B,βp)..U(C,γ1)\) corresponding to the edge \(\left\langle j,k\right\rangle\) corresponds to a subgraph \(g\left(j,k\right)\) with qubits \(j\) and \(k\) and the qubits whose distance from the qubits \(j\) and \(k\) in the graph is less than or equal to \(p\). Hence, in equation (5) each edge \(\left\langle j,k\right\rangle\) in the sum is associated with a subgraph \(g\left(j,k\right)\) and contributes to \(F_p\left(\gamma,\beta\right)\) as described below:
Note that the above expectation involves only the qubits in the graph \(g\left(j,k\right)\), and it does not depend on \(n\) or \(m\). Besides, this introduces a level of optimization, as for each edge \(\left\langle j,k\right\rangle\), we just need to evaluate a subgraph that is \(p\) steps away from the edge \(\left\langle j,k\right\rangle\) than the whole graph. Hence the complexity is \(p\) dependent than \(n\) dependent. So, the algorithm can give a speedup if \(p\) is fixed or grows slowly with \(n\).
Furthermore, if two or more subgraphs are isomorphic, then the angles \(\gamma\) and \(\beta\) are the same for them. Hence the subgraphs can be classified into certain unique types. With this, we can rewrite equation ( 5 ):
where \(g\) is the set of all subgraph types, \(w_g\) is the total number of subgraphs of a given type. This step optimizes the algorithm a bit. Since there could be isomorphic subgraphs, it is enough to evaluate them once and multiply with the total number of occurrences of the subgraph type.
The total number of qubits required to represent subgraph peaks if the subgraph is a tree. For a graph with a maximum degree \(v\), the number of qubits [5] in the tree is given by:
which is again \(n\) and \(m\) independent.
The goal of the quantum algorithm is to find the best possible angles \(\left(\gamma,\beta\right)\), which maximizes \(F_p\). The algorithm starts with a set of angles \(\left(\gamma,\beta\right)\), and a given value for \(p\) and the QAOA state outlined in equation ( 15 ) in the previous section is constructed. The circuit is then executed, and the qubits are measured in the computational basis producing the string \(z\). With this value \(C\left(z\right)\) is evaluated. Repeating this \(m\log{m}\) times gives a sample of \(C\left(z\right)\) values between \(0\) and \(+m\) with the mean of \(F_p\left(\gamma,\beta\right)\). An outcome of at least \(F_p\left(\gamma,\ \beta\right)-1\) will be obtained with probability \(1\ – 1/m\).
Now, let us examine how to implement the operator \(U(C_{\left\langle j,k\right\rangle},γ)\). Implementing \(U\left(B,\beta\right)\) should be straight forward, and we showed that earlier. From equations ( 7 ) in the previus section and ( 3 ), and ( 2 ), for the edge \(\left\langle j,k\right\rangle\):
We shall now study the effect of the term \(e^{-i\gamma\frac{1}{2}\left(-\sigma_z^j\sigma_z^k\right)}\) on an equal superposition state of the edge \(\left\langle j,k\right\rangle\). We know that from equation ( 2 ) in the previous section,
Applying \(e^{-i\gamma\frac{1}{2}\left(-\sigma_z^j\sigma_z^k\right)}\),
Each term in this operator \(e^{-i\gamma\frac{1}{2}\left(-\sigma_z^j\sigma_z^k\right)}\) can be implemented using \(CNOT\) and \(R_z\) gates, as shown in the following figure:
We first start with an equal superposition state of the edge \(\left\langle j,k\right\rangle\).
The next step is to apply a \(CNOT\) gate, with qubit \(j\) as the control and \(k\) as the target.
The second step is to apply the rotation operator \(R_z\left(\gamma\right)\) to the qubit \(k\). Recall that \(R_z\left(\gamma\right)\left.\left|x\right.\right\rangle=\ e^\frac{-i\gamma}{2}U_1\left(\gamma\right)\left.\left|x\right.\right\rangle=\ e^\frac{-i\gamma}{2}\left.e^{i\gamma x}\left|x\right.\right\rangle.\) The above equation can be written as:
The final step is to apply the CNOT gate one more time with qubit \(j\) as the control and \(k\) as the target. We get,
We can easily verify that the equation ( 15 ) and ( 10 ) are the same. Hence, we can infer that the quantum circuit implements \(e^{-i\gamma\frac{1}{2}\left(-\sigma_z^j\sigma_z^k\right)}\).
The second part of the equation ( 9 ), adds a phase \(e^\frac{-i\gamma}{2}\), which can be implemented as an \(R_x\left(\gamma\right)\) gate over state \(\left.\left|0\right.\right\rangle\), as shown in the figure, however, it is usually treated as an irrelevant constant.
Note
Be sure to use your API token and your account name. This module requires Scikit optimizer. If you have not installed it before, use the following command:
pip install scikit-optimize
Step 1. Import the required modules and obtain the backend
import QuantumRingsLib
from QuantumRingsLib import QuantumRegister, AncillaRegister, ClassicalRegister, QuantumCircuit
from QuantumRingsLib import QuantumRingsProvider
from QuantumRingsLib import job_monitor
from QuantumRingsLib import JobStatus
from matplotlib import pyplot as plt
from skopt import gp_minimize
import numpy as np
import math
provider = QuantumRingsProvider(token =<YOUR_TOKEN_HERE>, name=<YOUR_ACCOUNT_NAME_HERE>)
backend = provider.get_backend("scarlet_quantum_rings")
shots = 100
provider.active_account()
Step 2. Define the core methods
# define the operator U(B, beta)
def Operator_UB(graph, beta,qc, q, n_qubits):
for i in range(n_qubits): qc.rx(2*beta, q[i])
# define the operator U(C,gamma)
def Operator_UC(graph, gamma, qc, q, n_qubits):
for edge in graph:
qc.cx(q[edge[0]], q[edge[1]])
# multiply the gamma by the weight of the edge
qc.rz(gamma*edge[2], q[edge[1]])
qc.cx(q[edge[0]], q[edge[1]])
# a helper routine that computes the total weight of the cuts
def WeightOfCuts(bitstring):
totalWeight = 0
for edge in graph:
if bitstring[edge[0]] != bitstring[edge[1]]:
totalWeight += edge[2]
return totalWeight
def jobCallback(job_id, state, job):
#print("Job Status: ", state)
pass
# Builds the QAOA state.
def qaoaState( x, graph, p, n_qubits, expectationValue = True, shots=1024):
gammas = []
betas = []
# setup the gamma and beta array
for i in range(len(x)//2):
gammas.append(x[i*2])
betas.append(x[(i*2)+1])
# Create the quantum circuit
q = QuantumRegister(n_qubits)
c = ClassicalRegister(n_qubits)
qc = QuantumCircuit(q, c)
# First set the qubits in an equal superposition state
for i in range(n_qubits):
qc.h(q[i])
# Apply the gamma and beta operators in repetition
for i in range(p):
# Apply U(C,gamma)
Operator_UC(graph, gammas[i], qc, q, n_qubits)
# Apply U(B, beta)
Operator_UB(graph, betas[i],qc, q, n_qubits)
# Measure the qubits
for i in range(n_qubits):
qc.measure(q[i], c[i])
# Execute the circuit now
job = backend.run(qc, shots=shots)
job.wait_for_final_state(0, 5, jobCallback)
counts = job.result().get_counts()
# decide what to return
if ( True == expectationValue ):
# Calculate the expectation value of the measurement.
expectation = 0
for bitstring in counts:
probability = float(counts[bitstring]) / shots
expectation += WeightOfCuts(bitstring) * probability
del results
del job
return( expectation )
else:
# Just return the counts return(counts)
del results
del job
return(counts)
Step 3. Helper routines
def plot_histogram (counts, title=""):
"""
Plots the histogram of the counts
Args:
counts (dict):
The dictionary containing the counts of states
titles (str):
A title for the graph.
Returns:
None
"""
fig, ax = plt.subplots(figsize =(10, 7))
plt.xlabel("States")
plt.ylabel("Counts")
mylist = [key for key, val in counts.items() for _ in range(val)]
unique, inverse = np.unique(mylist, return_inverse=True)
bin_counts = np.bincount(inverse)
plt.bar(unique, bin_counts)
maxFreq = max(counts.values())
plt.ylim(ymax=np.ceil(maxFreq / 10) * 10 if maxFreq % 10 else maxFreq + 10)
# Show plot
plt.title(title)
plt.show()
return
Step 4. Put everything together and execute the code
p = 2 # Number of circuit layers
n_calls = 100 # Optimization cycles
n_random_starts = 2 # See scikit documentation
dimensions = [] # Search space, place holder
# Some example 2-regular graphs to play with, having equal weights.
# Each graph is a list of edges and their weights.
graph = [(0, 1, 1.0), (0, 3, 1.0), (1, 2, 1.0), (2, 3, 1.0)]
#graph = [(0,1,1.0), (0,5,1.0), (1,2,1.0), (2,3,1.0), (3,4,1.0), (4,5,1.0)]
# Find the number of qubits required.
n_qubits = 0
for i in range (len(graph)):
for j in range (2):
n_qubits = max(graph[i][j], n_qubits)
n_qubits += 1
# Construct the search space depending upon the circuit layers
for i in range(p):
dimensions.append((0,2*np.pi))
dimensions.append((0,np.pi))
d = tuple(dimensions)
# setup the optimization function, as its negative
f = lambda x: -1*qaoaState(x, graph, p, n_qubits)
# Use the Bayesian optimization using Gaussian Processes from Scikit optimizer
# to maximize the cost function (by minimizing its negative)
res = gp_minimize(func=f,
dimensions = d,
n_calls=n_calls,
n_random_starts=n_random_starts)
# Fetch the optimal gamma and beta values
x = res.x
# Execute the qaoa state with the optimal gamma and beta values
counts = qaoaState(x, graph, p, n_qubits, False)
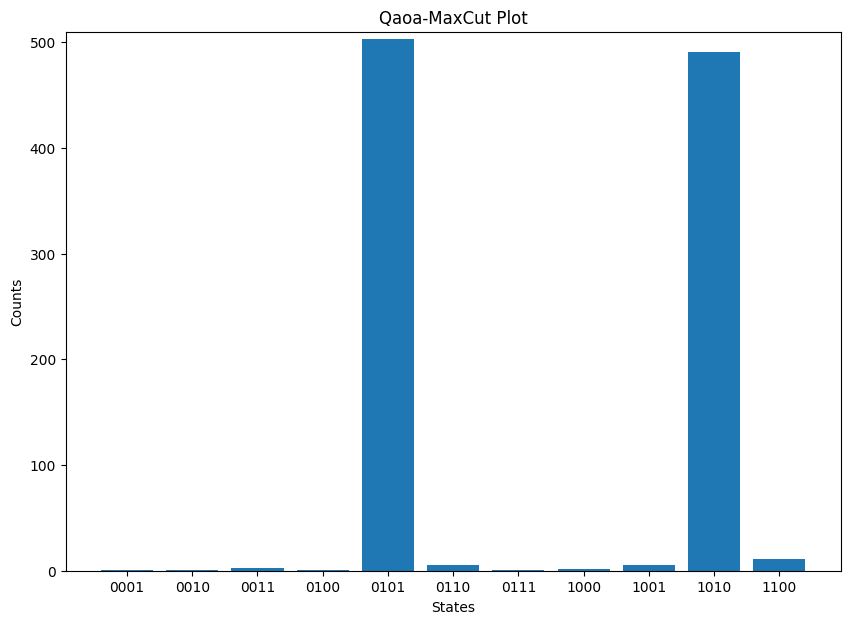
plot_histogram(counts,bar_labels=False,title='Qaoa-MaxCut Plot',number_to_keep=4)
Upon execution, you can expect a graph similar to the following graph, which can be classically interpreted. Beware that it takes a while to execute this code.
Footnotes